Проверим для каждого уравнения достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели

I уравнение	–1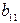
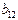
II уравнение		–1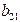
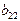
III уравнение			–1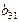
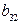
Тождество				–1

В соответствии с достаточным условием идентификации ранг матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, должен быть равен числу эндогенных переменных модели без одного.

Первое уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид

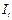
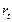
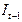
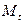
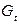
II уравнение	–1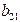
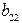
III уравнение		–1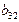
Тождество

Ранг данной матрицы равен трем, так как определитель квадратной подматрицы 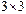не равен нулю:

.

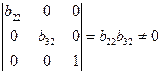Достаточное условие идентификации для данного уравнения выполняется.

Второе уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид

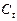
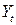
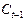
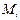
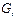
I уравнение	–1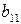
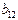
III уравнение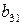
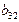
Тождество		–1

Ранг данной матрицы равен трем, так как определитель квадратной подматрицы 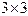не равен нулю:

.

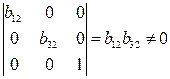Достаточное условие идентификации для данного уравнения выполняется.

Третье уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид

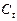
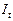
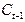
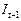
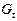
I уравнение	–1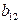
II уравнение		–1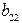
Тождество

Ранг данной матрицы равен трем, так как определитель квадратной подматрицы 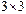не равен нулю:

.

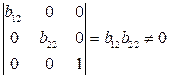Достаточное условие идентификации для данного уравнения выполняется.

Таким образом, все уравнения модели сверхидентифицируемы. Приведенная форма модели в общем виде будет выглядеть следующим образом: