Циклоидные кривые (рулеты). Определение, характеристика и способы построения

Циклоидные кривые (рулеты) — это кривые, которые являются траекторией движения точки окружности, которая без скольжения катится по прямой или по второй окружности. В первом случае кривую называют циклоидой. Если подвижная окружность (образующий круг) размещена вне подвижной окружности (направляющий круг), то кривую называют эпициклоидой, а если внутри, то — гипоциклоидой.

На рис. 13.58 показано построение точек циклоиды. За один оборот образующей окружности, точка А снова окажется на прямой l в точке А₈ на расстоянии - πd от ее начального положения. Поделим это расстояние, как и окружность, на произвольное количество одинаковых частей, например на восемь. Через точки деления окружности проведем горизонтальные прямые, а в точках деления О₁... О₈, горизонтальной прямой, которая инцендентна центру окружности, проведем дуги равные радиусу дуги, образующей окружности. Точки циклоиды лежат на пересечении соответствующих прямых и дуг. Нормаль к циклоиде в заданной точке А₃ соединяет эту точку с точкой соприкосновения 3', соответствующей ей окружности и прямой, при этом касательная перпендикулярная к нормали.

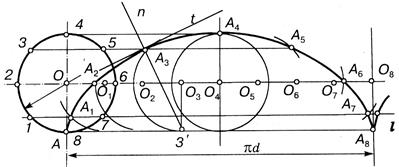
Рисунок 13.58

Если точка А лежит на радиальном луче образующей окружности, но внутри или извне его, то получают укороченные или продленные циклоиды, которые называют трохоидами.

Для построения точек эпициклоиды (рис.13.59, д) определяют центральный угол α по формуле α = R₁ • 360°/R, где R₁ — радиус образующей окружности; R — радиус дуги направляющей окружности. Потом дугу, инцендентную центру образующей окружности, в границах угла α разделяют, как и саму образующую окружность, на восемь равных частей. Точки эпициклоиды лежат на пересечении дуг, проведенных из центра направляющей окружности через точки деления образующей окружности, и соответствующих дуг образующей окружности, проведенных из точек деления О₁... О₈. Построение нормали и касательной показан на рис. 13.59, а.

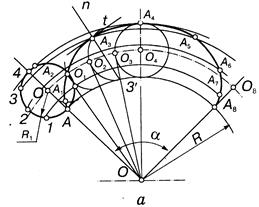
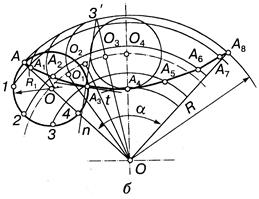
Рисунок 13.59

В AutoCAD построение циклоиды требует выполнения целого комплекса операций. Подробный ход построения циклоиды дается в примере построения очерки прокладки.

В зависимости от соотношения радиусов образующего и направляющего кругов эпициклоида имеет разное количество точек на недвижной окружности. Если R₁ = R, то эпициклоида имеет одну точку и называется кардиоидой (рис. 13.60). Укороченные или продленные кардиоиды называют завитками Паскаля. Если радиус образующей окружности равняется 1/2, 1/3, 1/4 и т.п. радиуса направляющей окружности, то таких точек соответственно 2, 3, 4 и т.д.

Построение точек гипоциклоиды (рис. 13.59, б) аналогично построению точек эпициклоиды. Центральный угол α определяют так же, как и для эпициклоиды.

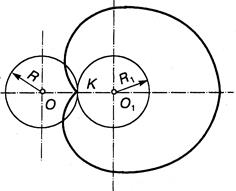
Рисунок 13.60

Укороченные или продленные гипоциклоиды называют гипотрохоидами. Количество точек на недвижимом круге зависит от соотношений радиусов образующего и недвижимого кругов. На рис. 13.61 показана гипоциклоида, для которой R/R₁ = 1/3. Гипоциклоида, для которой R/R₁ = 1/4, называют астроидой. Если R/R₁ = 1/2, то имеем отрезок прямой.

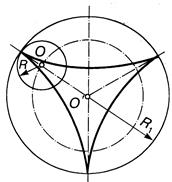
Рисунок 13.61

Построение точек эвольвенты окружности. Эвольвентой(разверткой) окружности называется кривая, которую описывает точка прямой линии, катящейся без скольжения по недвижной окружности (рис. 13.62). Чтобы построить множество точек эвольвенты, окружность разделяют на произвольное количество (например, на восемь) равных частей. Из каждой точки деления проводят касательную к окружности, на котором откладывают отрезок, который равняется длине дуги окружности от начальной точки к заданной. Полученная точка принадлежит эвольвенте.

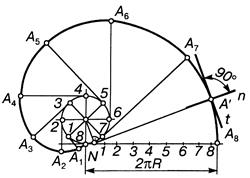
Рисунок 13.62

Относительно эвольвенты недвижная окружность является эволютой, то есть геометрическим местом центров кривизны эвольвенты. Отрезок от точки окружности к точке эвольвенты равняется радиусу кривизны эвольвенты.

Нормаль к эвольвенте в произвольной точке А' является касательной к недвижной окружности из точки А (способ построения — см. рис. 13.43).

Эвольвента является базисной кривой при профилировании зубцов одноименного зацепления зубчатых колес.

В AutoCAD построение эвольвенты требует выполнения целого комплекса операций. Подробный ход построения эвольвенты дается в примере построения очерка прокладки.

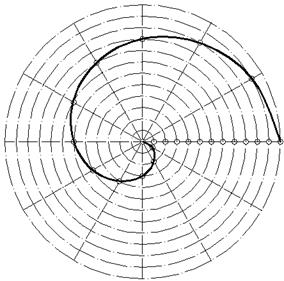
Построение точек спирали Архимеда. Спиралью Архимеда называют кривую, образованную траекторией точки, которая равномерно двигается вдоль радиус-вектора, который, в свою очередь, равномерно оборачивается вокруг неподвижного центра (рис. 13.63). Расстояния, на которое переместится точка от центра за один оборот радиуса - вектора, есть шагом спирали. Спираль имеет две ветви в зависимости от направления обращения радиус-вектора (по или против движения стрелки часов).

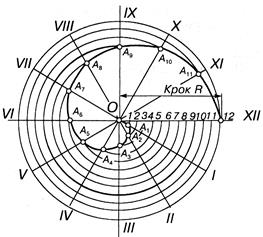
Рисунок 13.63

Если задан шаг спирали, то для построения его точек проводят круг радиусом, который равняется шагу, и разделяют шаг спирали и круг на произвольное количество равных частей. Точки спирали лежат на пересечении радиальных лучей, которые соединяют точки деления окружности и его центр, и дуг кругов, проведенных через соответствующие точки деления шага спирали (рис. 13.63).

Спираль Архимеда применяют в технике, проектируя самоцентрирующие патроны, кулачковые механизмы, эксцентрику и прочие устройства.

В AutoCAD спираль Архимеда строят с помощью сплайна. На рисунке штрихпунктирными линиями показаны вспомогательные концентрические окружности, имеющих общий центр. Их строят таким образом, чтобы они делили опорный отрезок, равный шагу спирали, на произвольное число равных частей. Далее из центра окружностей строят диаметры, показанные на рисунке штриховыми линиями. Они должны разделить окружности на одинаковые сектора; их число должно быть равным числу частей опорного отрезка. Сплайн строят, начиная из центра, по точкам пересечения окружностей и диаметров.

Построение точек синусоиды. Синусоида - это плоская кривая, образованная траекторией точки конца радиуса-вектора, который равномерно оборачивается вокруг центра и одновременно равномерно поступательно перемещается вдоль оси Ох. Синусоида есть графиком тригонометрической функции 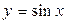в прямоугольной декартовой системе координат (рис. 13.64).

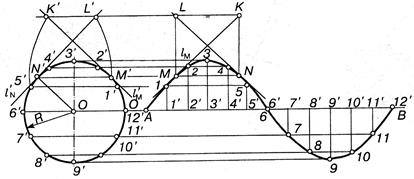
Рисунок 13.64

Способ построения точек синусоиды базируется на способе его образования. Круг заданного диаметра, что равняется амплитуде синусоиды (максимальному значению ординаты), разделяют на произвольное количество равных частей. На продолжении горизонтального диаметра окружности откладывают произвольный отрезок, который отвечает периоду синусоиды, и разделяют его на такое же количество равных частей. Точки синусоиды находят как пересечение горизонтальные прямых, проведенных через точки деления окружности, и вертикальные прямых, проведенных через точки деления отрезка периода синусоиды (рис. 13.64).

Для построения касательной в произвольной точке N находят соответствующую ей точку N' на круге и симметричные им точки М и М'. Через точку М' проводят эвольвенту окружности к пересечению с касательной, что проходит через точку N'. Точку пересечения L' проецируют на вертикальную прямую, проведенную через точку М. Получают точку L, которую соединяют с N. Это и есть касательная. Так же строят касательную в симметричной точке М. Этот способ построения касательной к синусоиде базируется на свойствах винтовой линии.

Синусоиды применяют при анализе колебательных процессов, в кулачковых механизмах и т.п.

Спирали, циклоидные кривые, синусоиды есть бесконечными трансцендентными кривыми, то есть такими, что не могут быть описанными алгебраическими уравнениями в прямоугольной декартовой системе координат.

В AutoCAD синусоиду строят с помощью сплайна по нескольким узловым точкам. Исходную окружность делят на произвольное число точек, например на 12, как это показано на рисунке, и с помощью выровненного размера определяют расстояние d между ними. На продолжении горизонтального диаметра выбирают точку А и от неё откладывают 12 отрезков, равных d. Через точки окружности в ортогональном режиме проводят 7 отрезков. Через 13 точек пересечения вспомогательных отрезков проводят сплайн, ориентируясь по примеру.

Построение точек конхоиды. Рассмотрим построение еще одной кривой - конхоиды. Конхоида имеет две ветви. Точки конхоиды лежат на радиусах-векторах и удаленные на одинаковом расстоянии от точек пересечения этих радиусов-векторов с произвольной кривой. Если эта кривая является прямой (рис. 13.65), то получим конхоиду Никомеда.

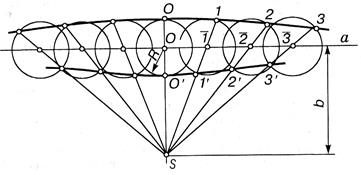
Рисунок 13.65

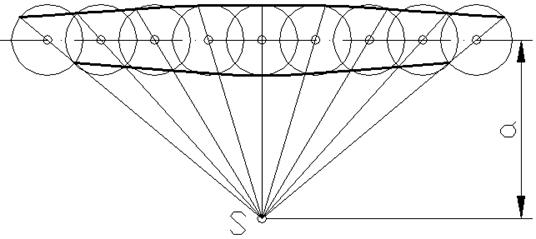
В AutoCAD конхоиду строят с помощью двух сплайнов. От узловой точки S на расстоянии а строят ось будущей конхоиды. В центре этой оси строим первую опорную окружность с радиусом R. Затем массивом копируем эту окружность в обе стороны. Расстояние между центрами опорных окружностей должно быть одинаковым, его задают произвольно. Затем из точки S строят вспомогательные отрезки через центры опорных окружностей. Точки пересечения опорных окружностей и вспомогательных отрезков соединяют двумя сплайнами.