Для измерения тесноты связи между факторным и результативным признаками рассчитывают специальные показатели – эмпирический коэффициент детерминации 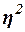 и эмпирическое корреляционное отношение
и эмпирическое корреляционное отношение 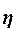 .
.
Эмпирический коэффициент детерминации 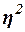 оценивает, насколько вариация результативного признака Y объясняется вариацией фактора Х (остальная часть вариации Y объясняется вариацией прочих факторов). Показатель
оценивает, насколько вариация результативного признака Y объясняется вариацией фактора Х (остальная часть вариации Y объясняется вариацией прочих факторов). Показатель 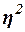 рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле
рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле
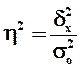 , (9)
, (9)
где 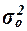 – общая дисперсия признака Y,
– общая дисперсия признака Y,
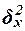 – межгрупповая (факторная) дисперсия признака Y.
– межгрупповая (факторная) дисперсия признака Y.
Значения показателя 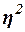 изменяются в пределах
изменяются в пределах 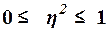 . При отсутствии корреляционной связи между признаками Х и Y имеет место равенство
. При отсутствии корреляционной связи между признаками Х и Y имеет место равенство 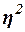 = 0, а при наличии функциональной связи между ними - равенство
= 0, а при наличии функциональной связи между ними - равенство 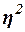 = 1.
= 1.
Общая дисперсия 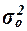 характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных). Этот показатель вычисляется по формуле
характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных). Этот показатель вычисляется по формуле
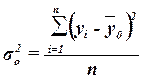 , (10)
, (10)
где yi – индивидуальные значения результативного признака;
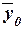 – общая средняя значений результативного признака;
– общая средняя значений результативного признака;
n – число единиц совокупности.
Общая средняя 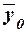 вычисляется как средняя арифметическая простая по всем единицам совокупности:
вычисляется как средняя арифметическая простая по всем единицам совокупности:
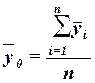 (11)
(11)
или как средняя взвешенная по частоте групп интервального ряда:
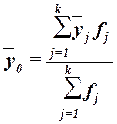 (12)
(12)
Для вычисления 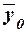 удобно использовать формулу (11), т.к. в табл. 8 (графы 3 и 4 итоговой строки) имеются значения числителя и знаменателя формулы.
удобно использовать формулу (11), т.к. в табл. 8 (графы 3 и 4 итоговой строки) имеются значения числителя и знаменателя формулы.
Расчет 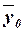 по формуле (11):
по формуле (11):
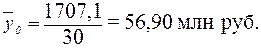
Для расчета общей дисперсии 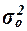 применяется вспомогательная таблица 12.
применяется вспомогательная таблица 12.
Таблица 12
Вспомогательная таблица для расчета общей дисперсии
| Номер банка п/п | Прибыль, млн руб. | 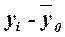 | 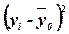 | 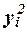 |
| 45,1 | -11,803 | 139,3187 | 2034,01 | |
| 6,2 | -50,703 | 2570,8280 | 38,44 | |
| 67,0 | 10,097 | 101,9427 | 4489,00 | |
| 27,3 | -29,603 | 876,3573 | 745,29 | |
| 62,5 | 5,597 | 31,3227 | 3906,25 | |
| 60,0 | 3,097 | 9,5893 | 3600,00 | |
| 16,9 | -40,003 | 1600,2667 | 285,61 | |
| 20,9 | -36,003 | 1296,2400 | 436,81 | |
| 65,0 | 8,097 | 65,5560 | 4225,00 | |
| 16,0 | -40,903 | 1673,0827 | 256,00 | |
| 69,0 | 12,097 | 146,3293 | 4761,00 | |
| 35,0 | -21,903 | 479,7560 | 1225,00 | |
| 53,4 | -3,503 | 12,2733 | 2851,56 | |
| 66,2 | 9,297 | 86,4280 | 4382,44 | |
| 56,0 | -0,903 | 0,8160 | 3136,00 | |
| 58,0 | 1,097 | 1,2027 | 3364,00 | |
| 47,0 | -9,903 | 98,0760 | 2209,00 | |
| 64,7 | 7,797 | 60,7880 | 4186,09 | |
| 46,2 | -10,703 | 114,5613 | 2134,44 | |
| 53,7 | -3,203 | 10,2613 | 2883,69 | |
| 67,0 | 10,097 | 101,9427 | 4489,00 | |
| 68,0 | 11,097 | 123,1360 | 4624,00 | |
| 70,0 | 13,097 | 171,5227 | 4900,00 | |
| 80,1 | 23,197 | 538,0853 | 6416,01 | |
| 67,7 | 10,797 | 116,5680 | 4583,29 | |
| 72,0 | 15,097 | 227,9093 | 5184,00 | |
| 84,0 | 27,097 | 734,2293 | 7056,00 | |
| 87,0 | 30,097 | 905,8093 | 7569,00 | |
| 90,2 | 33,297 | 1108,6680 | 8136,04 | |
| 85,0 | 28,097 | 789,4227 | 7225,00 | |
| Итого | 1707,1 | 1650,197 | 14192,2897 | 111331,97 |
Расчет общей дисперсии по формуле (10):
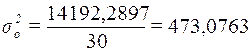
Общая дисперсия может быть также рассчитана по формуле
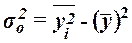 ,
,
где 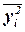 – средняя из квадратов значений результативного признака,
– средняя из квадратов значений результативного признака,
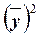 – квадрат средней величины значений результативного признака.
– квадрат средней величины значений результативного признака.
Для демонстрационного примера
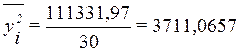
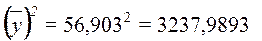
Тогда
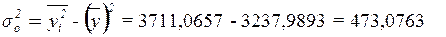
Межгрупповая дисперсия 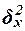 измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется в отклонении групповых средних
измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется в отклонении групповых средних 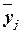 от общей средней
от общей средней 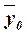 . Показатель
. Показатель 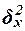 вычисляется по формуле
вычисляется по формуле
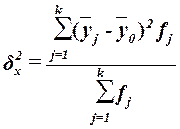 , (13)
, (13)
где 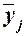 –групповые средние,
–групповые средние,
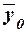 – общая средняя,
– общая средняя,
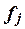 –число единиц в j-ой группе,
–число единиц в j-ой группе,
k – число групп.
Для расчета межгрупповой дисперсии 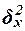 строится вспомогательная таблица 13 При этом используются групповые средние значения
строится вспомогательная таблица 13 При этом используются групповые средние значения 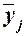 из табл. 8 (графа 5).
из табл. 8 (графа 5).
Таблица 13
Вспомогательная таблица для расчета межгрупповой дисперсии
| Группы банков по размеру кредитных вложений, млн руб. | Число банков, 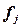 | Среднее значение 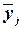 в группе в группе | 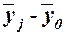 | 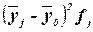 |
| 40 – 90 | 16,800 | -40,103 | 4824,8320 | |
| 90 – 140 | 40,216 | -16,687 | 1670,6690 | |
| 140 – 190 | 59,283 | 2,380 | 67,9728 | |
| 190 – 240 | 78,222 | 21,319 | 4090,4552 | |
| Итого | 10653,9291 |
Расчет межгрупповой дисперсии 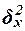 по формуле (11):
по формуле (11):
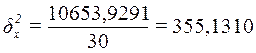
Расчет эмпирического коэффициента детерминации 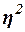 по формуле (9):
по формуле (9):
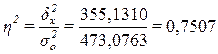 или 75,1%
или 75,1%
Вывод. 75,1% вариации суммы прибыли банков обусловлено вариацией объема кредитных вложений, а 24,9% – влиянием прочих неучтенных факторов.
Эмпирическое корреляционное отношение 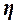 оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле
оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле
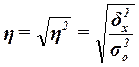 (14)
(14)
Значение показателя изменяются в пределах 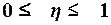 . Чем ближе значение
. Чем ближе значение 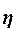 к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе
к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе 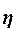 служит шкала Чэддока (табл. 14):
служит шкала Чэддока (табл. 14):
Таблица 14
Шкала Чэддока
| h | 0,1 – 0,3 | 0,3 – 0,5 | 0,5 – 0,7 | 0,7 – 0,9 | 0,9 – 0,99 |
| Характеристика силы связи | Слабая | Умеренная | Заметная | Тесная | Весьма тесная |
Расчет эмпирического корреляционного отношения 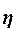 по формуле (14):
по формуле (14):
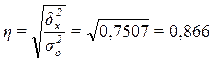 или 86,6%
или 86,6%
Вывод. Согласно шкале Чэддока связь между объемом кредитных вложений и суммой прибыли банков является тесной.
 2015-06-16
2015-06-16 5905
5905
