2015-06-16
849
Для расчета характеристик ряда распределения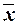 
, σ, σ 2, Vσ на основе табл. 5 строим вспомогательную таблицу 6 (
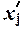– середина интервала).
Таблица 6
Расчетная таблица для нахождения характеристик ряда распределения
| Группы фирм по среднесписочной численности менеджеров, чел. | Середина интервала,
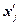
| Число фирм, fj |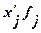 
| 
| 
| 
|
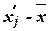
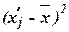
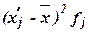
| 20-25 | 22,5 | 67,5 | -12,833 | 164,6859 | 494,0577 | |
| 25-30 | 27,5 | 110,0 | -7,833 | 61,3559 | 245,4236 | |
| 30-35 | 32,5 | 195,0 | -2,833 | 8,0259 | 48,1553 | |
| 35-40 | 37,5 | 375,0 | 2,167 | 4,6959 | 46,9589 | |
| 40-45 | 42,5 | 170,0 | 7,167 | 51,3659 | 205,4636 | |
| 45-50 | 47,5 | 142,5 | 12,167 | 148,0359 | 444,1077 | |
| ИТОГО | 1060,0 | 1484,16668 |
Рассчитаем среднюю арифметическую взвешенную:
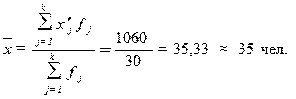
Рассчитаем среднее квадратическое отклонение:
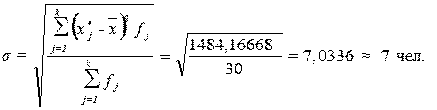
Рассчитаем дисперсию:
σ2= 7,03362= 49,47222
Рассчитаем коэффициент вариации:
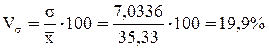
Вывод. Анализ полученных значений показателей 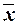и σ говорит о том, что средняя величина среднесписочной численности менеджеров составляет 35 чел., отклонение от этой величины в ту или иную сторону составляет в среднем 7 чел. (или 19,9%), наиболее характерная среднесписочная численность менеджеров находится в пределах от 28 до 42 чел. (диапазон 
).
|
|
|
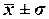Значение Vσ = 19,9% не превышает 33%, следовательно, вариация среднесписочной численности менеджеров в исследуемой совокупности фирм незначительна и совокупность по данному признаку однородна. Расхождение между значениями 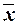, Мо и Ме незначительно ( 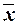=35 чел., Мо =37 чел., Ме =36 чел.), что подтверждает вывод об однородности совокупности фирм. Таким образом, найденное среднее значение среднесписочной численности менеджеров (35 чел.) является типичной, надежной характеристикой исследуемой совокупности фирм.
