Элементарные звенья и их характеристики

В общем случае звено САУ описывается линейным дифференциальным уравнением произвольного порядка вида (2.1)–(2.3) или соответствующей передаточной функцией (2.7). Введем понятие элементарного звена и покажем, что любое звено может быть представлено в виде совокупности элементарных звеньев.

Передаточная функция (2.7) есть отношение двух полиномов порядка m и n соответственно. Каждый из полиномов всегда можно представить в виде произведения простых сомножителей вида 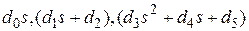, где сомножитель 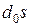соответствует нулевому корню уравнений B (s) = 0 или A (s) = 0, 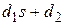–действительному корню, 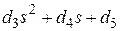– паре комплексно-сопряженных корней.

Исходя из этого, введем в рассмотрение элeмeнтaрные звeнья со следующими передаточными функциями: ; ; ; ; ; ; .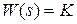

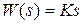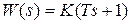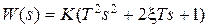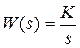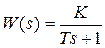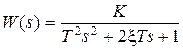Обозначим произвольную передаточную функцию элементарного звена через 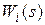. Нетрудно показать, что звено с передаточной функцией W (s) можно представить в виде

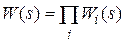или 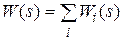. (2.17)

Представление W (s) в виде (2.17) оказывается удобным при вычислении и построении соответствующих характеристик звена, если известны характеристики элементарных звеньев. Действительно, из (2.17) нетрудно получить полезные соотношения:

если 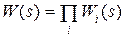, то , , ;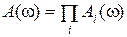

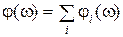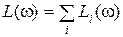если 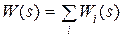, то , .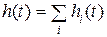

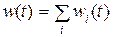Перейдем к рассмотрению характеристик элементарных звеньев.

Идeальноe усилитeльноe (бeзынepционноe или пpопоpциональноe) звено. Егоуравнение и передаточная функция имеют вид 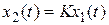, , 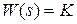(полагаем 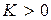), а частотные характеристики – , , , .

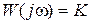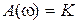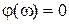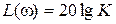Временные характеристики звена таковы: , .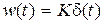

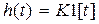Графики частотных и временных характеристик вполне очевидны.

Идeальноe интeгpиpующee звeно. Дифференциальное уравнение и передаточная функция имеют вид , , .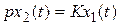

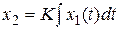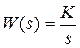Характеристики звена определяются следующими выражениями: 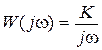, , 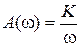, , 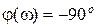, , 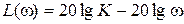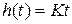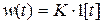графики которых, за исключением последней, представлены на рис. 2.7.

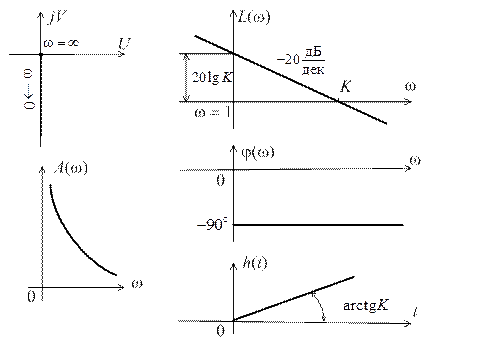
рис. 2.7

Идeальноe дифференцирующееe звeно. Звено имеет следующие дифференциальное уравнение и передаточную функцию: 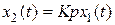, 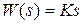и соответственно характеристики: 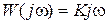, , 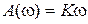, , 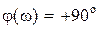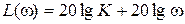графики которых представлены на рис. 2.8. Временные характеристики определяются выражениями , .

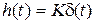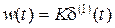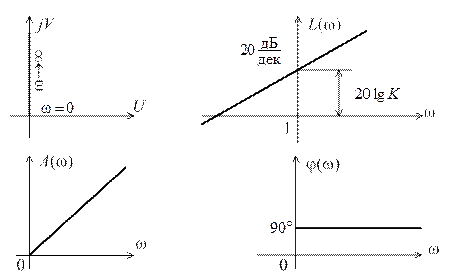
Рис. 2.8

Aпepиодичeскоe (инepционноe) звeно пepвого поpядка. Дифференциальное уравнение звена имеет вид .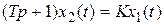

Передаточная функция и частотные характеристики имеют вид

, , ,

, .

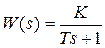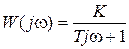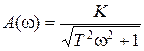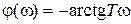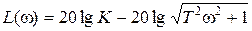Весовая и переходная функции звена определяются выражениями

, ,

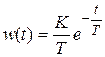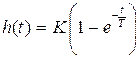графики которых представлены на рис. 2.9.

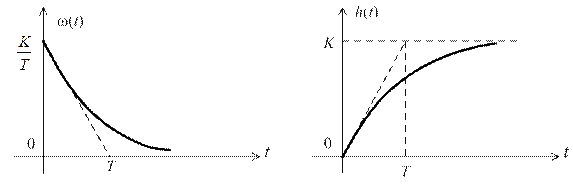
Рис. 2.9

На рис. 2.10 изображены частотные характеристики звена W (j ω), A (ω), 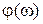. При этом годограф вектора 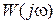представляет собой полуокружность.

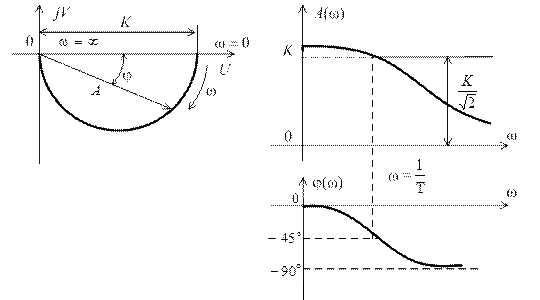
рис. 2.10

ЛАЧХ 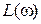может быть построена по приведенному выше выражению по точкам. Однако возможен более простой способ построения приближенной или асимптотической ЛАЧХ в виде отрезков прямых линий с наклонами: 0 до частоты 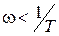и –20 дБ на декаду после частоты 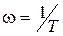. Соответствующий график приближенной (асимптотической) ЛАЧХ приведен на рис. 2.11, там же представлена и ЛФЧХ.

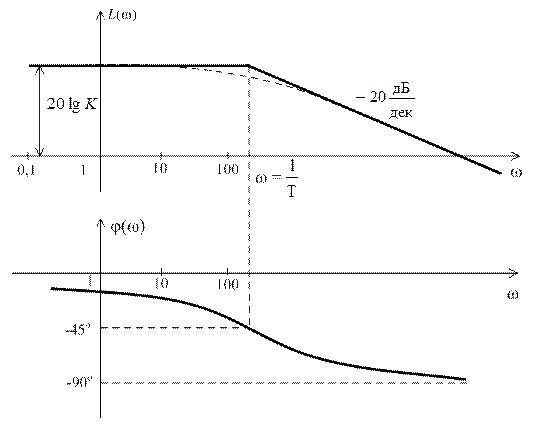
Рис. 2.11

Штриховой линией показан точный график 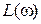. Максимальная ошибка 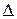между точным графиком 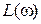и асимптотическим будет при 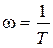и составит

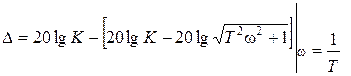
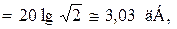
что вполне допустимо.

Колeбатeльноe звeно. Дифференциальное уравнение колебательного эвена имеет вид

.

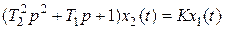Будем полагать, что 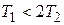, тогда корни характеристического уравнения 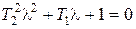будут комплексными. Чаще передаточную функцию звена записывают в ви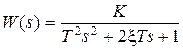де , где , , .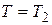

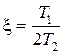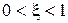Частотные и временные характеристики звена имеют следующий вид:

; ;

,

, ,

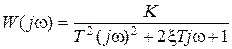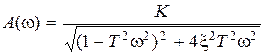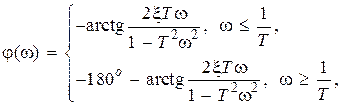
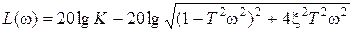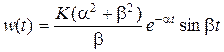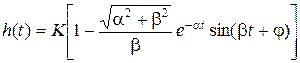где , , .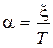

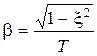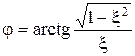Анализ АЧХ показывает, что 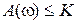для любого 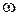, есл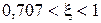и . При 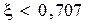на графике 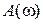появляется «горб», который уходит в бесконечность при 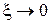. Величину 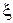называют параметром затухания. Чем меньше 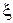, тем медленнее затухает колебательная составляющая в выражениях w (t) и h (t).

Асимптотическая ЛАЧХ в виде ломаной может быть получена только при 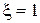и имеет следующий вид: .

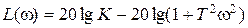Переход от прямой с наклоном 0 дБ/дек на прямую с наклоном –40 дБ/дек происходит на частоте излома 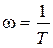. Считается, что такую аппроксимацию можно использовать 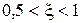при . При 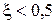в окрестностях точки 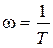на ЛАЧХ также появляется «гopб». В этом случае при построении 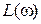в диапазоне 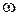, близких к 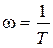, следует использовать точное выражение для 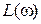или воспользоваться специальными номограммами.

Графики частотных характеристик колебательного звена приведены на рис. 2.12, а временных характеристик – на рис. 2.13.

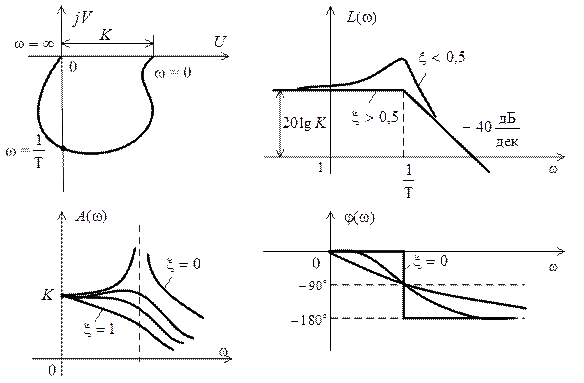
рис. 2.12

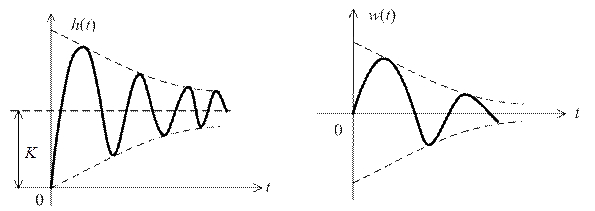
рис. 2.13

Частные случаи колебательного звена: консepвативноe звeно при 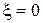,имеющее передаточную функцию 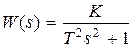, и апериодическое звено второго поpядка при 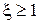,передаточная функция которого равна

, .

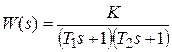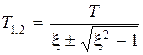Фоpсиpующеe звeно пepвого поpядка. Дифференциальное уравнение и передаточная функция звена имеют вид 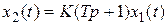, , 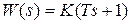а частотные и временные характеристики определяются выражениями

, , , , , .

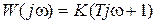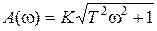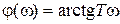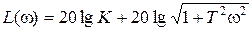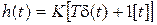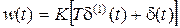Графики частотных характеристик представлены на рис. 2.14.

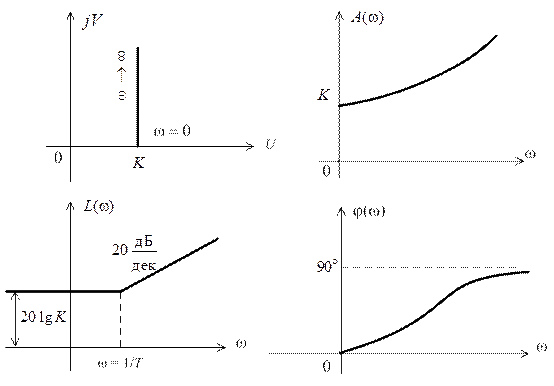
Рис. 2.14

Фоpсиpующeе звeно второго поpядка. Диффференциальное уравнение и передаточная функция равны соответственно 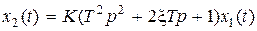, 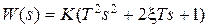при услови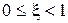и . При 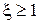это звено можно представить как произведение двух элементарных форсирующих звеньев первого порядка.