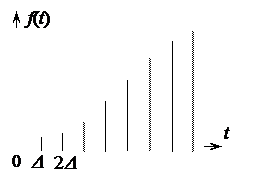Элементарные сигналы

При решении некоторых инженерных задач относительно сложные радиотехнические сигналы оказывается целесообразным представить в виде суммы (суперпозиции) более простых так называемых элементарных сигналов. Например, при анализе прохождения сигналов через линейные цепи необходимо бывает рассчитать форму сигнала на выходе цепи. Это можно сделать, представив входной сигнал в виде суммы очень простых элементарных сигналов, результат прохождения которых через исследуемую цепь известен или его легко найти. Наиболее употребительными элементарными сигналами являются: функция включения (единичный скачок), дельта-функция и гармонический сигнал.

Функция включения (функция Хэвисайда) (рис. 1.1, а) описывается выражением

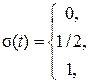
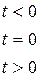. (1.1)

Ее можно рассматривать как предельный переход при q ® 0 функции s (t), изображенной на рис. 1.1, б.

б

а

Рис. 1.1. Функция Хэвисайда (а) и ее приближение (б)

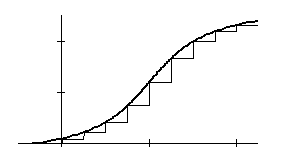
Произвольный сигнал можно представить в виде суперпозиции функций включения, как показано на рис. 1.2.

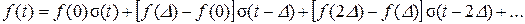
Рис. 1.2. Представление произвольного сигнала с помощью функций Хэвисайда

Если теперь шаг D устремить к нулю, то дискретную переменную kD можно заменить непрерывной переменной t, а скачки сигнала f (kD) – f ((k – 1) D) превращаются в дифференциал d f = (d f /d t)d t, в результате чего получается формула представления сигнала в виде суперпозиции функций Хэвисайда:

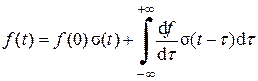. (1.2)

В курсе основ теории цепей вводится понятие переходной характеристики как реакции цепи на единичный скачок на входе. Иначе говоря, если на вход цепи подать сигнал в виде единичного скачка s(t), то на выходе получится сигнал в виде переходной характеристики g (t). Зная переходную характеристику, легко найти сигнал на выходе цепи при действии на ее входе произвольного сигнала f (t), например, представленного на рис. 1.2. В результате действия каждого элементарного скачка s(t – kD), умноженного на высоту соответствующей ступеньки, на выходе будет получаться сигнал g (t – kD), умноженный на такую же высоту ступеньки. В итоге можно легко получить выражение для выходного сигнала, заменив в формуле (1.2) s(t) на g (t):

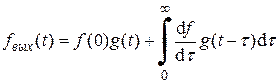. (1.3)

Это выражение является хорошо известной формулой интеграла Дюамеля.

Дельта-функция (функция Дирака) – это очень своеобразный математический объект. Она равна нулю при всех значениях аргумента кроме t = 0, а при t = 0 она равна бесконечности:

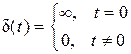. (1.4)

Кроме того, d-функция удовлетворяет дополнительному условию:

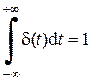. (1.5)

Дельта-функцию можно рассматривать как предельный случай очень короткого импульса единичной площади (рис. 1.3). Если устремить длительность такого импульса к нулю при неизменной площади, то в пределе получим
d-функцию:

.

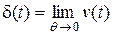Поскольку d-функция имеет единичную площадь, ее размерность – 1/с.

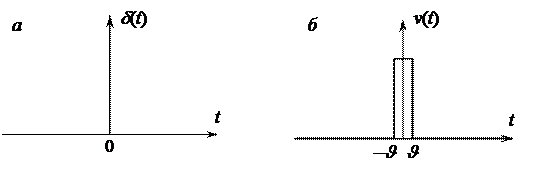Рис. 1.3. Дельта-функция (а) и ее приближение (б)

Дельта-функция связана с функцией включения простым соотношением. Нетрудно видеть, что функция v (t), изображенная на рис. 1.3, равна производной от функции s (t) на рис. 1.1, б:

v (t) = d s (t)/d t.

Полагая q ® 0, получаем

d(t) = ds(t)/d t. (1.6)

Дельта-функцию принято изображать графически в виде вертикальной стрелки (см. рис. 1.3, а).

Очевидно, что сигнал в виде идеальной d-функции реально существовать не может. Однако d-функция оказывается очень удобной математической моделью при описании коротких импульсов. Произвольный сигнал можно рассматривать как суперпозицию коротких импульсов, как показано на рис. 1.4.

.

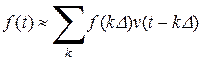Устремляя D ® 0, получаем:

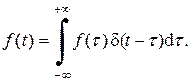(1.7)

Рис.1.4. Представление произвольного сигнала в виде суперпозиции коротких импульсов

Если на вход линейной цепи подать d-функцию, то сигнал на ее выходе называется импульсной характеристикой h (t). Если же на вход подать произвольный сигнал (рис. 1.4), составленный из очень коротких импульсов, то каждый из этих коротких импульсов породит на выходе цепи сигнал, пропорциональный импульсной характеристике. В результате выходной сигнал может быть представлен в виде

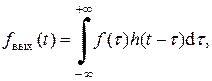(1.8)

т. е. сигнал на выходе цепи равен свертке входного сигнала и импульсной характеристики цепи.

Дельта-функция обладает еще одной примечательной особенностью, которую называют фильтрующим свойством. Если она входит в состав подынтегрального выражения, то такие интегралы очень легко вычисляются. Математически это выражается следующим образом:

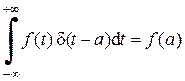. (1.9)

Интеграл от некоторой функции f (t), умноженной на d-функцию, равен значению подынтегральной функции f (t) в той точке, где d-функция обращается в бесконечность.

Гармонический сигнал (рис. 1.5) описывается математическим выражением

u (t) = U_m cos (w ₀ t + j).

Гармонические сигналы получили широкое распространение в радиотехнике благодаря следующим отличительным качествам.

1. Это единственный вид сигнала, который не изменяет своей формы при прохождении через любую линейную систему. Изменяется только амплитуда и фаза сигнала на выходе.

2. Собственные колебания колебательных контуров и других резонансных устройств имеют вид гармонической функции. Благодаря этому гармонические сигналы разных частот легко отфильтровывать друг от друга.

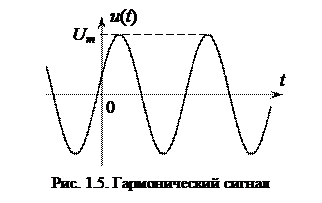3. Гармонические сигналы можно генерировать с помощью относительно простых устройств.

В течение почти ста лет с момента изобретения радио гармонические сигналы были почти единственным видом сигналов, который использовался в качестве несущего колебания при передаче информации по радиоканалам. И хотя в последние годы в связи с развитием цифровой техники наряду с гармоническими сигналами стали использоваться другие виды сигналов, значение гармонических сигналов в радиотехнике по-прежнему остается чрезвычайно высоким.

Контрольные вопросы

1. Что такое элементарные сигналы? Для чего они используются?

2. Назовите основные свойства дельта-функции.

3. Как понимать, что интеграл от дельта функции равен единице?

4. В чем состоит фильтрующее свойство дельта-функции?

5. Какова связь между функцией Хэвисайда и дельта-функцией?

6. Чем обусловлено широкое применение гармонических сигналов в радиотехнике?