Найти первую производную неявной функции и функции, заданной параметрически.
а) 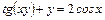 ; б)
; б) 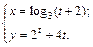
Решение.
a) Считая 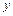 функцией от
функцией от 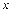 , дифференцируем обе части равенства по
, дифференцируем обе части равенства по 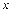 :
:
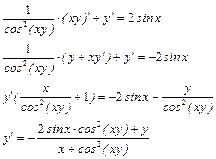
б) Используем формулу 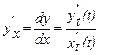 при параметрическом дифференцировании:
при параметрическом дифференцировании:
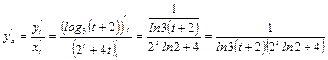
ЗАДАЧА 19 Найти наименьшее и наибольшее значение функции 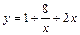 на отрезке
на отрезке 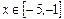 .
.
Найдем критические точки из условия равенства нулю 1-ой производной:
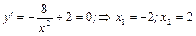 .
. 
Так как 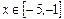 , то эту критическую точку не учитываем. Чтобы выяснить, имеет ли функция экстремум в точке
, то эту критическую точку не учитываем. Чтобы выяснить, имеет ли функция экстремум в точке 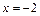 , найдём
, найдём 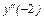 :
:
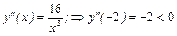 ,
,
т.е. в точке 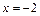 функция имеет максимум. Находим значения функции в точках
функция имеет максимум. Находим значения функции в точках 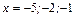 :
:
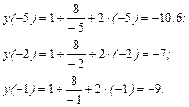
Т.е. минимальное значение 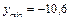 функция принимает на левом конце отрезка, а максимальное
функция принимает на левом конце отрезка, а максимальное 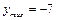 внутри отрезка при
внутри отрезка при 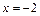 .
.
 2015-06-16
2015-06-16 152
152







