Решение. Обозначим , тогда уравнение примет вид

Обозначим 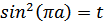, тогда уравнение примет вид:

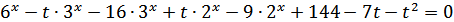
Сгруппируем:

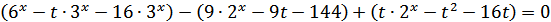
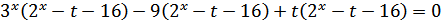
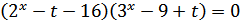
Таким образом:

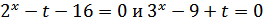
1. Рассмотрим первый корень: 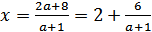. Подставим его в первое равенство:

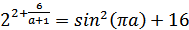
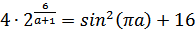
Функция, стоящая слева убывает, приближаясь к 4 сверху при a → ∞ и снизу при a → −∞. Функция, стоящая справа – постоянная величина, принимающая значения из отрезка [16;17].

Таким образом, возможен единственный корень, и корень этот легко найти подбором a = 2.

Подставим найденное значение а во второй корень .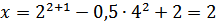

Проверим является ли это число корнем первого уравнения:

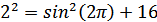
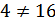
не является корнем.

Проверим является ли это число корнем второго уравнения:

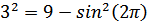
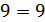
является корнем.

2. Подставим первый корень во второе равенство:

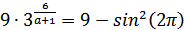
Функция, стоящая слева убывает, приближаясь к 9 сверху при a → ∞ и снизу при a → −∞.

Функция, стоящая справа – постоянная величина, принимающая значения из отрезка [8;9].

Таким образом, корень может быть, но при отрицательных a. Но тогда второй корень во втором равенстве дает a = 2, а в первом при положительных a. Противоречие.

Ответ: а=2.

C5 Найти все значения параметра а, при которых выражение 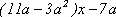больше выражения 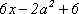при любом значении х, принадлежащем промежутку (2, 5).