Решение

Преобразуем:

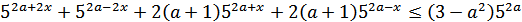
Разделим на 5^2а:

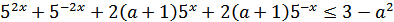
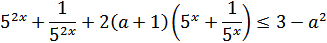
Пусть 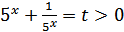, тогда: 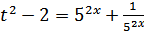. Неравенство примет вид:

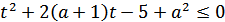
Это парабола, ветви вверх, значит решения не будет если квадратный трехчлен не имеет корней (дискриминант меньше нуля):

r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">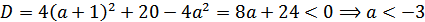

Решений также не будет, если оба корня этого квадратного уравнения не положительные. Из теоремы Виета можно сделать вывод, что это будет выполнено, когда t < 0, но это невозможно.

Еще возможен случай, когда корней вовсе нет. Тогда: 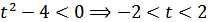причем при t = 2 корень есть х=0.

Таким образом, решений не будет если все решения попадут в интервал: 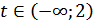. Для этого необходимо выполнение условий:

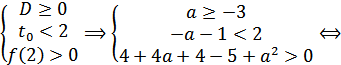
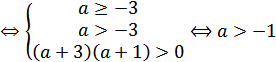
Ответ: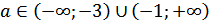

C5 Найдите все значения a > 0, при каждом из которых 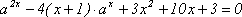имеет на отрезке [-1; 2] ровно два корня.