Рассмотрим теперь пример сравнения с помощью критерия Пирсона 2х экспериментальных распределений.
Одинаков ли уровень подготовки учащихся в 2х школах, если в первой школе из 100 человек поступили в ВУЗ 82, а во второй – из 87 – 44.
Решение: Представим данные задачи в виде 4х польной таблицы.
| 1 - я | 2 - я | |
| поступившие | ||
| Не поступившие | ||
| Сумма |
Найдём так называемую долю признака или частоту поступления
Р = 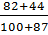
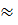 0,67
0,67
Подсчитаем теперь сколько учащихся из первой и второй школ должны были поступить в ВУЗ.
1 –я:0,67*100 = 67
2 – я: 0,67*87 = 58,29
Найдём теперь сколько учащихся не должно было поступить.
1 – я: 100 – 67 = 33
2 – я: 87 – 58,29 = 28,71
Составим теперь таблицу теоретических частот
| 1 -я | 2 - я | |
| Поступили | 58,29 | |
| Не поступили | 28,71 | |
| Сумма |

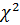 =
= 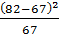 +
+ 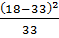 +
+ 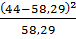 +
+ 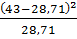
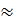 20,9
20,9
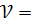 (2 -1) (2 – 1) = 1
(2 -1) (2 – 1) = 1
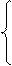 3,841,р = 0,05 0,05 0,01
3,841,р = 0,05 0,05 0,01
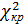 = не значим. Значим. Неопред.
= не значим. Значим. Неопред.




 6,635, р = 0,01
6,635, р = 0,01
3,841 6,635 20,9
Таким образом, следует принять гипотезу о наличии различий между двумя эмпирическими распределениями. Отсюда следует вывод о том, что уровень подготовки в 2х школах различается.
 2015-06-04
2015-06-04 811
811








