1. Егер 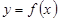 функциясы
функциясы 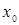 нүктесінде дифференциалданатын болса, онда бұл функция осы нүктеде үзіліссіз.
нүктесінде дифференциалданатын болса, онда бұл функция осы нүктеде үзіліссіз.
Шынымен де, 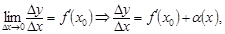 мұндағы
мұндағы 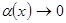 , егер
, егер 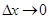 . Бұдан,
. Бұдан,
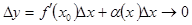 , егер
, егер 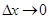 .
.
2. Күрделі функциялардың туындылары. Егер 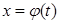 функциясы
функциясы 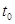 нүктесінде диф-ференциалданатын, ал
нүктесінде диф-ференциалданатын, ал 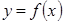 функциясы
функциясы 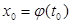 нүктесінде дифференциалданатын болса, онда
нүктесінде дифференциалданатын болса, онда 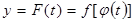 күрделі функциясы
күрделі функциясы 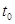 нүктесінде дифференциалданады және
нүктесінде дифференциалданады және
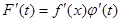 , немесе
, немесе 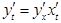
3. Кері функцияның туындысы. Егер 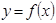 функциясы үшін
функциясы үшін 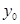 нүктесінде туындысы бар және ол нөлден өзгеше болатындай
нүктесінде туындысы бар және ол нөлден өзгеше болатындай 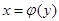 кері функциясы табылса, онда
кері функциясы табылса, онда
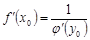 .
.
4. 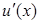 және
және 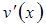 табылсын, ал
табылсын, ал 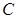 - const. Онда
- const. Онда
1. а) 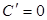 . Шынында да, 2. . Шынында да, 2. 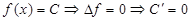 . б) . б) 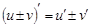 . . | 3. в) 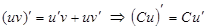 . г) . г) 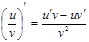 . . |
3.Туындының кестесі
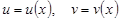 -
- 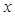 айнымалысына тәуелді функциялар, ал
айнымалысына тәуелді функциялар, ал 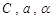 - тұрақты сандар болсын. Онда
- тұрақты сандар болсын. Онда
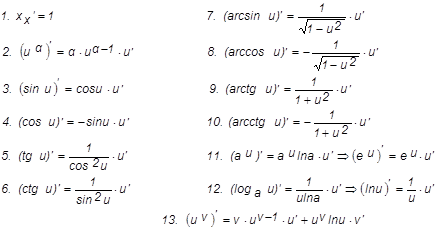
3-формуланың дәлелдеуін келтірелік.
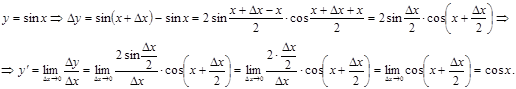
Мысал 2. Берілген функциялардың туындыларын тап:
а) 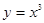 . 2-ші формуладан
. 2-ші формуладан 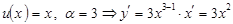 .
.
б) 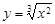 .
. 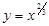 . 2-ші формуладан
. 2-ші формуладан 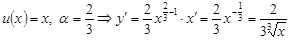 .
.
в) 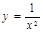 .
. 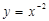 . 2-ші формуладан
. 2-ші формуладан 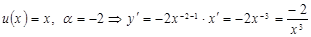 .
.
г) 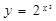 . 11-ші формуладан
. 11-ші формуладан 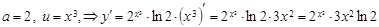 .
.
3.1 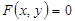 айқын емес функциясын дифференциалдау
айқын емес функциясын дифференциалдау
Берілген функцияның туындысын табу үшін 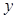 -тің
-тің 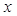 айнымалысына тәуелді функция екенін ескере отырып, теңдіктің екі жағын да дифференциалдаймыз.
айнымалысына тәуелді функция екенін ескере отырып, теңдіктің екі жағын да дифференциалдаймыз.
Мысал 3. 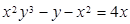 функциясының туындысын тап.
функциясының туындысын тап.
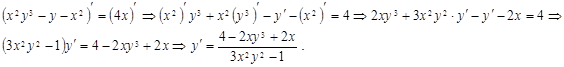
3.2 Параметрлік түрде берілген функцияның туындысы
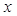 айнымалысына тәуелді
айнымалысына тәуелді 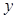 функциясы параметрлік түрде берілсін
функциясы параметрлік түрде берілсін
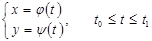 .
.
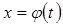 функциясының кері функциясы бар болып,
функциясының кері функциясы бар болып, 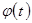 және
және 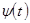 функциялары дифференциалданатын функциялар, сонымен қатар,
функциялары дифференциалданатын функциялар, сонымен қатар, 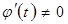 болсын. Онда
болсын. Онда 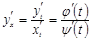 .
.
Мысал 4. 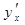 тап.
тап.
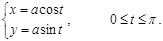
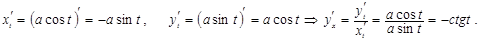
1. Функцияның дифференциалы
2.
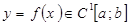 болсын. Онда
болсын. Онда 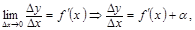 мұндағы
мұндағы 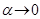 , егер
, егер 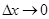 . Бұдан
. Бұдан 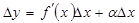 .
.
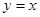 болсын. Онда
болсын. Онда 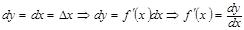 теңдіктерден төмендегі теңдікті аламыз:
теңдіктерден төмендегі теңдікті аламыз:
1. 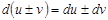 2. 2. 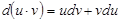 3. 3. 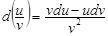 | 4. 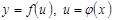 немесе немесе 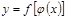 болсын. Онда болсын. Онда 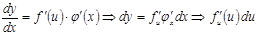 - бірінші дифферен-циалдың формасының инварианттылық қасиеті. 5. - бірінші дифферен-циалдың формасының инварианттылық қасиеті. 5. 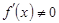 болса. болса. 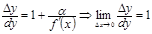 теңдігі орынды болғандық- тан, жуықтап есептеуде теңдігі орынды болғандық- тан, жуықтап есептеуде 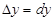 деп алуға болады, немесе деп алуға болады, немесе |
 (5)
(5)
Мысал 5. 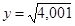 есепте.
есепте.
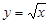 функциясын қарастыралық және
функциясын қарастыралық және 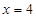 деп алайық.
деп алайық. 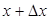 ретінде
ретінде 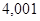 санын аламыз. Онда
санын аламыз. Онда 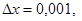
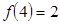 .
.
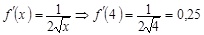 . Онда (5)-тен
. Онда (5)-тен 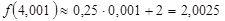 .
.
5. Туынды және жоғарғы дифференциалдар
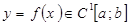 болсын. Егер
болсын. Егер 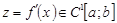 болса, онда
болса, онда 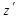
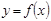 функциясының екінші ретті туындысы деп аталады және былай белгіленеді:
функциясының екінші ретті туындысы деп аталады және былай белгіленеді: 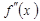 . Яғни
. Яғни
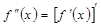 немесе
немесе 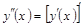
Анықтама 5. 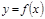 функциясының
функциясының 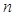 -ші ретті туындысы деп
-ші ретті туындысы деп 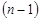 -ші ретті туындыдан алынған туындыны айтамыз, яғни,
-ші ретті туындыдан алынған туындыны айтамыз, яғни,
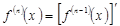
Мысал 6. 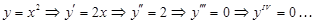
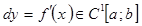 болсын. Онда
болсын. Онда 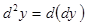
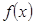 функциясының екінші ретті диф-ференциалы деп аталады. Бұдан
функциясының екінші ретті диф-ференциалы деп аталады. Бұдан
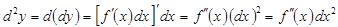 .
.
Анықтама 6. 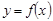 функциясының
функциясының 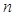 -ші ретті дифференциалы деп
-ші ретті дифференциалы деп 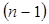 -ші ретті дифференциалды тағы бір рет дифференциалдауды айтамыз және
-ші ретті дифференциалды тағы бір рет дифференциалдауды айтамыз және
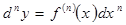 (6)
(6)
(6)-дан
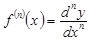 (7)
(7)
шығады. (6) және (7) теңдіктер 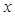 айнымалысы тәуелсіз айнымалы болған жағдайда ғана ақиқат.
айнымалысы тәуелсіз айнымалы болған жағдайда ғана ақиқат.
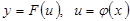 болсын. Онда
болсын. Онда 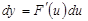 .
.
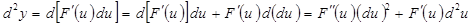 ,
,
яғни, дифференциалдың формасының инварианттылығы сақталмайды.
6. 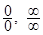 түріндегі анықталмағандықтарды ашу. Лопиталь ережесі.
түріндегі анықталмағандықтарды ашу. Лопиталь ережесі.
Мысал 7.
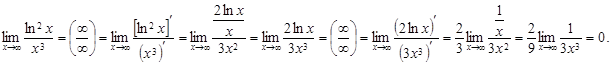 (8)-ші формулада сол жағында шек болуы мүмкін, ал оң жағында шек жоқ.
(8)-ші формулада сол жағында шек болуы мүмкін, ал оң жағында шек жоқ.
Мысал 8.
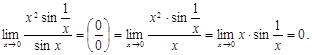
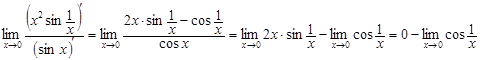 - шегі жоқ.
- шегі жоқ.
1.1 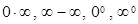 түріндегі анықталмағындықтарды ашу.
түріндегі анықталмағындықтарды ашу.
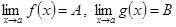 болсын. Онда
болсын. Онда
а) 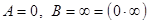 . Бұл жағдайда,
. Бұл жағдайда, 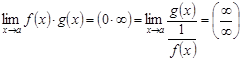 .
.
Мысал 9. 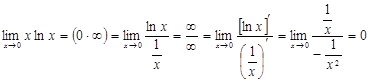 .
.
б) 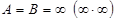 . Онда
. Онда 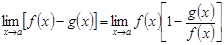 .
.
Мысал 10. 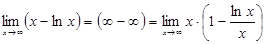 .
.
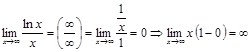 .
.
в)  өрнегінен алатынымыз
өрнегінен алатынымыз 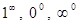 , және
, және 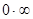 жағдайына келеміз. Егер теңдік-тің екі жағында логарифмдесек.
жағдайына келеміз. Егер теңдік-тің екі жағында логарифмдесек.
Мысал 11.
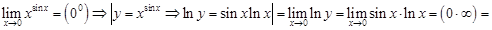
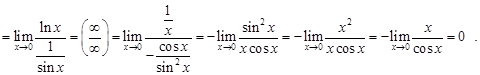
Немесе 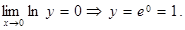
Өзін-өзі тексеруге арналған тест сұрақтары:
1. 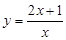 функциясының туындысын табыңыз:
функциясының туындысын табыңыз:
[А] 2
[В] 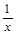
[С 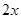
[Д] 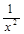
[Е] [+] 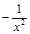 .
.
2. 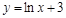 функциясының туындысын табыңыз:
функциясының туындысын табыңыз:
[А] [+] 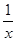
[В] 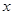
[С] 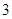
[Д] 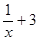
[Е] 
3. 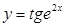 функциясының туындысын табыңыз:
функциясының туындысын табыңыз:
[А] 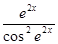
[В] 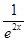
[С] [+] 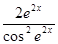
[Д] 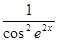
[Е] 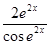
4. 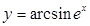 функциясының туындысын табыңыз:
функциясының туындысын табыңыз:
[А] 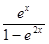
[В] 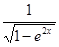
[С] 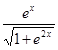
[Д][+] 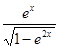
[Е] 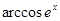
5. 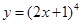 функциясының туындысын табыңыз:
функциясының туындысын табыңыз:
[А] [+] 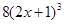
[В] 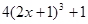
[С] 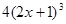
[Д] 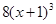
[Е] 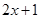
8-ші дәріс
 2015-06-04
2015-06-04 5251
5251








