Анықтама 5. Комплекс сан деп 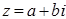 түріндегі өрнекті айтамыз, мұндағы
түріндегі өрнекті айтамыз, мұндағы 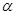 және
және 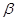 нақты сандар, ал
нақты сандар, ал 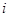
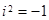 немесе
немесе 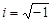 теңдіктерімен анықталатын жорамал бірлік, сонымен қатар,
теңдіктерімен анықталатын жорамал бірлік, сонымен қатар, 
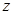 комплекс санының нақты бөлігі, ал
комплекс санының нақты бөлігі, ал 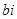 жорамал бөлігі деп аталады.?
жорамал бөлігі деп аталады.?
Егер 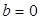 болса, онда
болса, онда 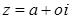 орнына
орнына 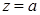 деп жазады және оның
деп жазады және оның 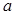 санынан ешбір айырмашылығы жоқ. Ендеше, нақты сандар комплекс санның дербес жағдайы.
санынан ешбір айырмашылығы жоқ. Ендеше, нақты сандар комплекс санның дербес жағдайы.
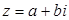 саны
саны 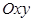 жазықтығында
жазықтығында 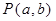 нүктесі болып бейнеленеді.
нүктесі болып бейнеленеді.
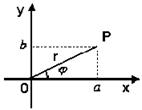 | 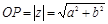 саны саны 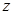 комплекс санының модулі деп, ал комплекс санының модулі деп, ал 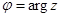  комплекс санының аргументі деп аталады. Комплекс сандар жиыны мен комплекс санының аргументі деп аталады. Комплекс сандар жиыны мен  жазықтығының нүктелерінің арасында өзара-бірмәнді сәйкестік бар. жазықтығының нүктелерінің арасында өзара-бірмәнді сәйкестік бар. 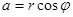 және және 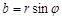 болғандықтан, болғандықтан, 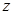 комплекс санын комплекс санын 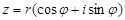 түрінде жазуға болады, бұл түрінде жазуға болады, бұл 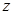 комплекс санының тригонометриялық формасы деп аталады. комплекс санының тригонометриялық формасы деп аталады. |
Комплекс сандар арасындағы амалдар 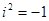 екені ескеріле отырып, жүргізіледі:
екені ескеріле отырып, жүргізіледі:
1. 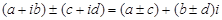 ,
,
2. 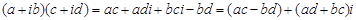 ,
,
3. 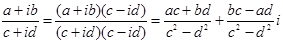 .
.
Тригонометриялық формадағы 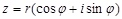 комплекс сандар үшін, яғни,
комплекс сандар үшін, яғни, 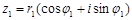 және
және 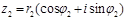 үшін төмендегі теңдік орынды:
үшін төмендегі теңдік орынды:
|
|
|
1. 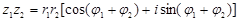 ,
,
2.  ,
,
3. 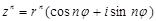 - Муавр формуласы,
- Муавр формуласы,
4. 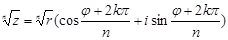 ,
, 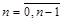 , яғни,
, яғни, 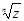 -нің әрқашанда әртүрлі
-нің әрқашанда әртүрлі 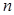 мәні бар.
мәні бар.
Анықтама 6. 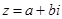 және
және 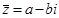 сандары түйіндес деп аталады және
сандары түйіндес деп аталады және 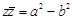 .
.
Теорема 1. Егер нақты коэффициентті көпмүшеліктің 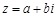 саны түбірі болса, онда
саны түбірі болса, онда 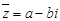 саны да осы көпмүшеліктің түбірі болады.
саны да осы көпмүшеліктің түбірі болады.
Мысал 1. 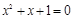 квадрат теңдеуін шеш.
квадрат теңдеуін шеш.
Дискриминант табамыз: 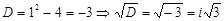 . Онда
. Онда
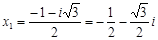 ,
, 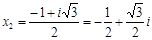
1-ші мысалдан байқайтынымыз, квадрат теңдеудің әрқашанда екі түбірі болады: нақты немесе комплекс. Егер оның түбірі комплекс сан болса, оның екінші түбірі осы комплекс санның түйіндесі болады.
Ары қарай бізге төмендегі көрсеткіштік функция қажет болады:
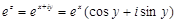 .
.
Егер 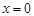 болса, кәдімгі көрсеткіштік
болса, кәдімгі көрсеткіштік 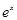 функциясын аламыз, ал егер
функциясын аламыз, ал егер 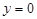 болса, онда Эйлер формуласын аламыз
болса, онда Эйлер формуласын аламыз
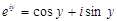
2. Нақты айнымалы функция
 қандай да бір
қандай да бір  кеңістігіндегі нүктелер жиыны болсын.
кеңістігіндегі нүктелер жиыны болсын.
Анықтама1. Егер әрбір 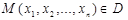 нүктесіне (әрбір
нүктесіне (әрбір 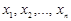 айнымалыларының жұптары үшін)
айнымалыларының жұптары үшін) 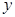 айнымалысының анықталған белгілі бір мәні сәйкестікке қойылса, онда
айнымалысының анықталған белгілі бір мәні сәйкестікке қойылса, онда 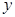
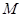 нүктесінің
нүктесінің 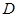 жиынындағы функциясы деп аталады (
жиынындағы функциясы деп аталады (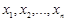
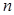 тәуелсіз айнымалының функциясы) және былай белгіленеді
тәуелсіз айнымалының функциясы) және былай белгіленеді
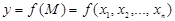 ,
, 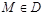 ,
,
мұндағы 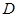
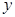 функциясының анықталу облысы деп аталады.
функциясының анықталу облысы деп аталады.
Егер әрбір 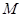 нүктесіне
нүктесіне 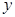 -тің тек бір ғана мәні сәйкестікке қойылса, онда
-тің тек бір ғана мәні сәйкестікке қойылса, онда 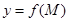 бірмәнді функция, кері жағдайда – көпмәнді функция болады.
бірмәнді функция, кері жағдайда – көпмәнді функция болады.
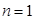 болғанда бір айнымалы функция аламыз
болғанда бір айнымалы функция аламыз 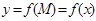 , мұндағы
, мұндағы 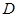 -ны көбінде
-ны көбінде 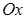 сандық түзуінің кесіндісі немесе интервалы ретінде қарастырамыз.
сандық түзуінің кесіндісі немесе интервалы ретінде қарастырамыз. 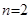 болса, екі айнымалы функцияны аламыз
болса, екі айнымалы функцияны аламыз 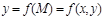 , мұндағы
, мұндағы 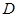 -ны көбінде
-ны көбінде 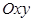 жазықтығының
жазықтығының 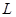 сызығымен (шекарасымен) шектелген бөлігі ретінде қарастырамыз. Егер
сызығымен (шекарасымен) шектелген бөлігі ретінде қарастырамыз. Егер 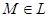 болса, онда
болса, онда 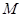 -
- 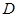 -ның шекаралық нүктесі, ал егер
-ның шекаралық нүктесі, ал егер 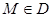 және
және 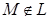 болса, онда
болса, онда 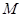 -
- 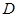 -ның ішкі нүктесі.
-ның ішкі нүктесі.
|
|
|
Егер 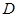 облысының құрамына оның шекаралық нүктелерінің барлығы енетін болса, онда оны тұйық облыс деп атаймыз, кері жағдайда – ашық облыс деп атады. Егер
облысының құрамына оның шекаралық нүктелерінің барлығы енетін болса, онда оны тұйық облыс деп атаймыз, кері жағдайда – ашық облыс деп атады. Егер 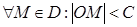 , орындалатындай
, орындалатындай 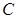 тұрақтысы табылатын болса, мұндағы
тұрақтысы табылатын болса, мұндағы 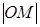 координаттың бас нүктесінен
координаттың бас нүктесінен 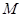 нүктесіне дейінгі ара қашықтық, онда
нүктесіне дейінгі ара қашықтық, онда 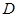 шектелген облыс деп аталады.
шектелген облыс деп аталады.
Функция әртүрлі түрде берілуі мүмкін, солардың негізгісі функцияның аналитикалық түрде берілуі (формула түрінде). Бұл жағдайда, көбінесе, әрине, функцияның анықталу облысын табу қажет болады.
Мысал 2. а) Бір айнымалы функциялар.
1. 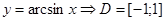 - тұйықталған облыс,
- тұйықталған облыс,
2. 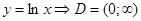 - ашық шексіз облыс.
- ашық шексіз облыс.
б) Екі айнымалы функциялар.
1. 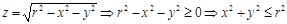 .
. 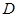 - центрі координатаның бас нүктесі, ал радиусы
- центрі координатаның бас нүктесі, ал радиусы 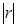 болатын тұйық дөңгелек.
болатын тұйық дөңгелек.
2. 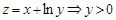 . Бұл жерде
. Бұл жерде 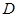 :
: 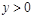 - жарты жазықтық, ашық шексіз облыс.
- жарты жазықтық, ашық шексіз облыс.
 үшін функцияның графигі ұғымын
үшін функцияның графигі ұғымын  -дегі
-дегі  координаталары
координаталары 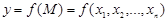 теңдігін қанағаттандыратын нүктелердің геометриялық орны деп енгізуге болады. 4-ші дәрісте көрсетілгендей, бір айнымалы функцияның графигі
теңдігін қанағаттандыратын нүктелердің геометриялық орны деп енгізуге болады. 4-ші дәрісте көрсетілгендей, бір айнымалы функцияның графигі 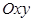 жазықтығындағы сызық, ал екі айнымалы функцияның графигі
жазықтығындағы сызық, ал екі айнымалы функцияның графигі 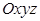 кеңістігіндегі бет.
кеңістігіндегі бет.
Бір айнымалы функцияларды қарастырайық.
Анықтама2. 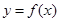 функциясы жұп функция [тақ функция] деп аталады, егер
функциясы жұп функция [тақ функция] деп аталады, егер 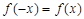
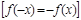 .?
.?
Жұп функцияның графигі 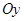 өсіне қарағанда симметриялы, ал тақ функцияның графигі координаталардың бас нүктесіне қарағанда симметриялы.
өсіне қарағанда симметриялы, ал тақ функцияның графигі координаталардың бас нүктесіне қарағанда симметриялы.
Мысал 3. 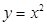 - жұп функция, ал
- жұп функция, ал 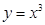 - тақ функция.
- тақ функция.
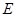 –
– 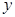 -тің өзгеру облысы, ал
-тің өзгеру облысы, ал 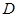 -
- 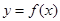 функциясының анықталу облысы болсын.
функциясының анықталу облысы болсын.
Анықтама.
3. 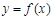 функциясы периоды
функциясы периоды 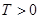 болатын периодты функция деп аталады, егер
болатын периодты функция деп аталады, егер 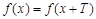 ,
, 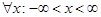 болса.
болса.
4. 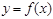 функциясы кемімейтін [өспелі] немесе өспелі емес [кемімелі] функция деп аталады, егер
функциясы кемімейтін [өспелі] немесе өспелі емес [кемімелі] функция деп аталады, егер 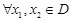 үшін
үшін 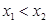 болғанда сәйкесінше
болғанда сәйкесінше 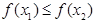
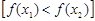 теңсіздігі орындалса немесе
теңсіздігі орындалса немесе 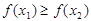
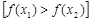 теңсіздігі орындалса. Бұл функциялар бірсарынды деп аталады.
теңсіздігі орындалса. Бұл функциялар бірсарынды деп аталады.
5. 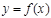 функциясы – бірмәнді функция. Онда
функциясы – бірмәнді функция. Онда 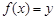 болатындай,
болатындай, 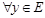 -ге сәйкестікке
-ге сәйкестікке 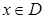 қоюға болады. Ендеше,
қоюға болады. Ендеше, 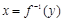 функциясы анықталған және ол
функциясы анықталған және ол 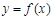 функциясына кері функция деп аталады.
функциясына кері функция деп аталады.
Мысал 4. 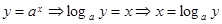 .
.
Егер кері функцияда 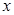 пен
пен 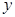 -тің орнын ауыстыратын болсақ, онда кері функцияның графиктері
-тің орнын ауыстыратын болсақ, онда кері функцияның графиктері 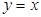 түзуіне қарағанда симметриялы.
түзуіне қарағанда симметриялы.
6. 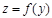 , ал
, ал 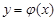 болсын. Онда
болсын. Онда 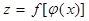 функциясын
функциясын 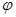 және
және 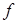 функцияларының суперпозициясы немесе күрделі функция деп атаймыз.
функцияларының суперпозициясы немесе күрделі функция деп атаймыз.
7. Функция 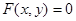 түрінде берілген болса, онда оны айқын емес функция деп атаймыз. Яғни,
түрінде берілген болса, онда оны айқын емес функция деп атаймыз. Яғни, 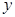 функциясы
функциясы 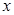 айнымалысы арқылы өрнектелмеген.
айнымалысы арқылы өрнектелмеген.
Мысал 5. 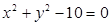 ,
, 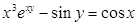 .
.
8. 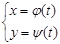 ,
, 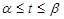 , жүйесі берілсін. (3)
, жүйесі берілсін. (3)
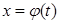 функциясының кері функциясы
функциясының кері функциясы 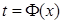 бар делік. Онда
бар делік. Онда 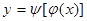 , яғни,
, яғни, 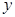
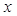 айнымалысына тәуелді функция. (3) жүйесі
айнымалысына тәуелді функция. (3) жүйесі 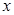 айнымалысына тәуелді
айнымалысына тәуелді 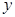 функциясының параметрлік түрде берілуі деп, ал
функциясының параметрлік түрде берілуі деп, ал 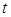 - параметр деп аталады.
- параметр деп аталады.
Мысал 6. 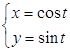
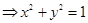 .
.
9. 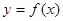 функциясы шектелген деп аталады, егер
функциясы шектелген деп аталады, егер 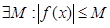
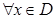 , мұндағы
, мұндағы 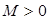 - тұрақты сан.
- тұрақты сан.
10. Негізгі элементар функцияларға мыналар жатады: 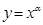 - дәрежеліе,
- дәрежеліе, 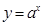 - көрсеткіштік,
- көрсеткіштік, 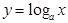 - логарифмдік,
- логарифмдік, 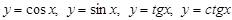 - тригонометрия-лық,
- тригонометрия-лық, 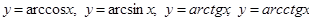 кері тригонометриялық функциялар.
кері тригонометриялық функциялар.
2.1 Декарттық координаталар жүйесіндегі бір айнымалы функциялардың графиктері
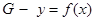 функциясының графигі. Онда функциялардың графиктері:
функциясының графигі. Онда функциялардың графиктері:
а) 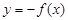
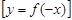 -
- 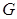 бейнесінің
бейнесінің 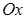 өсі бойынша шағылуы
өсі бойынша шағылуы 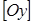 ,
,
б) 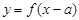
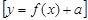 -
- 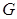 -ді
-ді  өсі бойымен оңға [
өсі бойымен оңға [  өсі бойымен жоғары]
өсі бойымен жоғары] 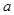
бірлік жылжыту;
в) 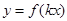
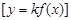 -
-  -ді
-ді 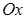 өсі бойымен
өсі бойымен 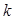 есе сығу немесе созу
есе сығу немесе созу 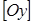 .
.
3. Полярлық координаталар жүйесі
Жазықтықтан кез келген бір 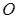 нүктесін аламыз және осы
нүктесін аламыз және осы  нүктесінен сәуле жүргіземіз (
нүктесінен сәуле жүргіземіз ( нүктесі – полюс, ал сәуле – полярлық өс) 1-сурет.
нүктесі – полюс, ал сәуле – полярлық өс) 1-сурет.
|
|
|
Онда жазықтықтағы кез келген нүктенің орны сандардың жұбы (полярлық координаталар) 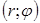 , мұндағы
, мұндағы 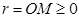 – полярлық радиус, ал
– полярлық радиус, ал 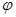 ,
, 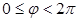 - полярлық бұрыш, яғни, полярлық өс пен
- полярлық бұрыш, яғни, полярлық өс пен 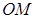 -нің арасындағы бұрыш. Ал координаталар жүйесін полярлық координаталар жүйесі деп атаймыз. Енді, полярлық координаталар жүйесі мен декарттық координаталар жүйесі арасындағы байланысты табалық. Полюс декарттық жүйелер координатасының бас нүктесімен, ал полярлық өс -
-нің арасындағы бұрыш. Ал координаталар жүйесін полярлық координаталар жүйесі деп атаймыз. Енді, полярлық координаталар жүйесі мен декарттық координаталар жүйесі арасындағы байланысты табалық. Полюс декарттық жүйелер координатасының бас нүктесімен, ал полярлық өс - 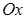 жарты түзуімен беттессін.
жарты түзуімен беттессін.
Онда 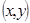 декарттық координаталар жүйесінен
декарттық координаталар жүйесінен 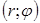 полярлық координаталар жүйесіне көшу:
полярлық координаталар жүйесіне көшу: 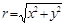 ,
, 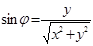 ,
, 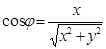 , ал керісінше,
, ал керісінше, 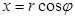 ,
, 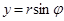 (2-сурет).
(2-сурет).
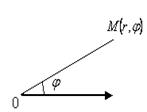 1-сурет. 1-сурет. | 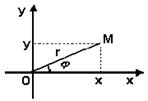 2-сурет. 2-сурет. | Полярлық координаталар жүйесінде кейбір қисықтардың теңдеулері ықшамды түрде болады:    . . |
3. Сандық тізбектер және оның шектері
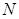 - натурал сандар жиыны,
- натурал сандар жиыны, 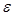 - тұрақты,
- тұрақты, 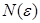 -
- 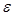 тұрақтысына тәуелді нөмір болсын.
тұрақтысына тәуелді нөмір болсын.
Анықтама:
11. Егер 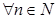 сәйкестікке
сәйкестікке 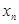 шамасы қойылса, онда
шамасы қойылса, онда 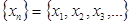 тізбегі берілген деп айтамыз.
тізбегі берілген деп айтамыз.
Сандық тізбектерді қарастырамыз, яғни, 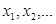 - сандар.
- сандар. 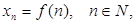 тізбегін функция деп есептеуге де болатыны анық, мұндағы
тізбегін функция деп есептеуге де болатыны анық, мұндағы 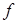 –
– 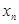 -ді
-ді 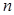 -ге сәйкестікке қою заңы:
-ге сәйкестікке қою заңы:
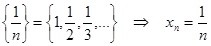 ,
, 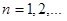
12. 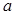 санын
санын 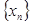 тізбегінің шегі деп айтамыз, егер
тізбегінің шегі деп айтамыз, егер 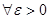 үшін
үшін
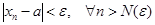 , (4)
, (4)
теңсіздігі орындалатындай 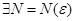 табылса және
табылса және 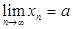
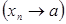 деп белгілейміз де,
деп белгілейміз де, 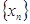
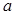 -ға ұмтылады (жинақталады) деп айтамыз.
-ға ұмтылады (жинақталады) деп айтамыз.
(4)-ті мына түрде жазуға болады: 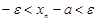
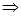
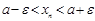
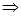
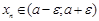 . Бұдан,
. Бұдан, 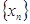 жинақты болады дегеннен
жинақты болады дегеннен 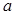 нүктесінің кез келген аймағының сыртқы жағында орналасқан
нүктесінің кез келген аймағының сыртқы жағында орналасқан 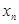 нүктелерінің жиыны ақырлынемесе бос, ал ішінде орналасқан
нүктелерінің жиыны ақырлынемесе бос, ал ішінде орналасқан 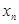 нүктелері-нің жиыны жиыны шектеусіз.
нүктелері-нің жиыны жиыны шектеусіз.
12-ші анықтамадан мынадай теореманы қорытындылауға болады:
Теорема 1. Жинақталған тізбек шектелген және оның тек бір ғана шегі бар.
Анықтама 13. Егер 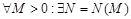 , мұндағы
, мұндағы 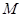 - тұрақты сан,
- тұрақты сан, 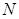 -
- 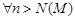 үшін
үшін 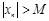 теңсіздігі орындалатын нөмір, онда
теңсіздігі орындалатын нөмір, онда 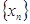 тізбегі
тізбегі 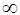 -ке ұмтылады деп айтамыз және
-ке ұмтылады деп айтамыз және 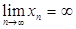 деп белгілейміз.
деп белгілейміз.
|
|
|
Теорема 2. Егер 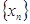 бірқалыпты болса, онда оның сәйкес жағынан шектеулі жинақтылықтың жеткілікті шарты.
бірқалыпты болса, онда оның сәйкес жағынан шектеулі жинақтылықтың жеткілікті шарты.
Мысал 6. Мынадай тізбекті қарастыралық: 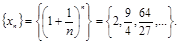
Ньютон биномын қолдана отырып, 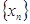 тізбегінің өспелі және жоғарғы жағынан 3 санымен шектелетіндігін көрсетуге болады. Онда 2-ші теоремадан оның жинақты екендігі шығады. Ол шекті
тізбегінің өспелі және жоғарғы жағынан 3 санымен шектелетіндігін көрсетуге болады. Онда 2-ші теоремадан оның жинақты екендігі шығады. Ол шекті 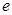 әріпімен белгілейміз, яғни,
әріпімен белгілейміз, яғни, 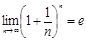 , мұндағы
, мұндағы 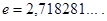
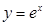 көрсеткіштік функциясы мен
көрсеткіштік функциясы мен 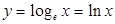 - натурал логарифмдік функция математикада өте жиі қолданылады.
- натурал логарифмдік функция математикада өте жиі қолданылады.
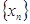 тізбегі берілсін. Осы тізбектен нөмірлері
тізбегі берілсін. Осы тізбектен нөмірлері 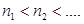 болатын элементтерің шектеусіз жиынын таңдап аламыз. Егер
болатын элементтерің шектеусіз жиынын таңдап аламыз. Егер 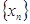 тізбегі
тізбегі 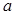 санына жинақталатын болса, онда оның кез келген
санына жинақталатын болса, онда оның кез келген 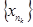 ішкі тізбегі де жинақты болып, оның шегі осы
ішкі тізбегі де жинақты болып, оның шегі осы 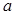 саны болады.
саны болады.
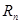 -дегі
-дегі 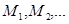 нүктелерінің тізбегін қарастыралық.
нүктелерінің тізбегін қарастыралық.
Анықтама 14. 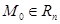 нүктесін
нүктесін 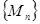 тізбегінің шегі деп айтамыз, егер
тізбегінің шегі деп айтамыз, егер 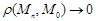 .
.
Сонымен, 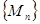 тізбегінің
тізбегінің 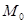 нүктесіне жинақталуы
нүктесіне жинақталуы 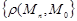 сандық тізбегінің нөл тұрақтысына жинақталуымен анықталады.
сандық тізбегінің нөл тұрақтысына жинақталуымен анықталады. 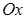 түзуінде
түзуінде 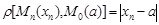 теңдігі орындалатындықтан, 12-ші анықтаманы
теңдігі орындалатындықтан, 12-ші анықтаманы 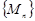
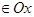 нүктелер тізбегінің
нүктелер тізбегінің 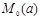 нүктесіне жинақты болу анықтамасы деп айта аламыз.
нүктесіне жинақты болу анықтамасы деп айта аламыз.
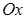 түзуінің бойындағы нүктелер тізбектерінің шегінің геометриялық интерпрета-циясын жалпылай отырып:
түзуінің бойындағы нүктелер тізбектерінің шегінің геометриялық интерпрета-циясын жалпылай отырып: 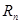 -дегі
-дегі 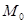 нүктесі
нүктесі 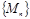 нүктелер тізбегінің шегі болады, сонда және тек сонда ғана, егер
нүктелер тізбегінің шегі болады, сонда және тек сонда ғана, егер 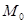 нүктесінің кез келген аймағында осы тізбектің қандай да бір нөмірден бастап, барлық нүктелері жататын болса.
нүктесінің кез келген аймағында осы тізбектің қандай да бір нөмірден бастап, барлық нүктелері жататын болса.
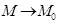 жазуын
жазуын 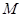 айнымалы нүктесінің координаталары барлық
айнымалы нүктесінің координаталары барлық 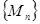 нүктелер
нүктелер 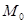 нүктесіне жинақталатын сәйкес координаталарының мәндерін ғана қабылдайды деп түсінеміз.
нүктесіне жинақталатын сәйкес координаталарының мәндерін ғана қабылдайды деп түсінеміз.
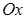 үшін:
үшін: 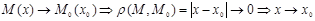 .
.
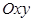 үшін
үшін 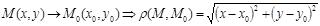
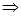
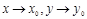 .
.
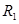 -дегі
-дегі 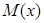 айнымалы нүктесінің
айнымалы нүктесінің 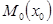 нүктесіне ұмтылуы тек
нүктесіне ұмтылуы тек 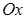 түзуі бойында ғана, ал
түзуі бойында ғана, ал 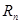 -де,
-де, 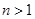
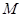 -нің
-нің 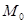 -ге ұмтылу жолы шексіз жиын.
-ге ұмтылу жолы шексіз жиын.
Өзін-өзі тексеруге арналған тест сұрақтары:
1. 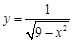 функциясының анықталу облысын табыңыз
функциясының анықталу облысын табыңыз
[А] 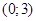
[В][+] 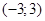
[С] 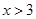
[Д] 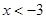
[Е] 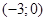
2. 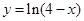 функциясының анықталу облысын табыңыз
функциясының анықталу облысын табыңыз
[А] 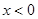
[В] 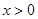
[С] [+] 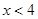
[Д] 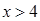
[Е] 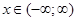
3. 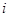 комплекстік саны мынадай көрсеткіштік түрде былай жазылады
комплекстік саны мынадай көрсеткіштік түрде былай жазылады
[А][+] 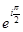
[В] 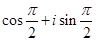
[С] 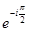
[Д] 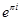
[Е] 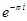
4. 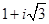 комплекстік саны мынадай тригонометриялық түрде жазылады
комплекстік саны мынадай тригонометриялық түрде жазылады
[А] 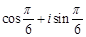
[В] 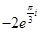
[С] 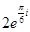
[Д] 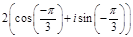
[Е][+] 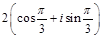
5. 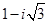 комплестік саны мынадай тригонометриялық түрде жазылады
комплестік саны мынадай тригонометриялық түрде жазылады
[А] 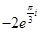
[В] 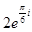
[С] 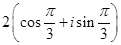
[Д][+] 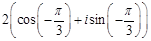
[Е] 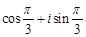
6-шы дәріс
Функцияның шегі. Үзіліссіз функциялар
1. Функцияның шегінің анықтамасы.
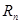 -дегі
-дегі 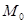 нүктесінің қандай да бір аймағында,
нүктесінің қандай да бір аймағында, 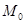 нүктесінің өзінде де,
нүктесінің өзінде де, 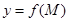 функциясы анықталған болсын.
функциясы анықталған болсын.
Анықтама.
1. (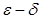 тілінде).
тілінде). 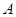 саны
саны 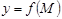 функциясының
функциясының 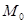 нүктесіндегі шегі деп аталады (
нүктесіндегі шегі деп аталады (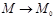 үшін), егер
үшін), егер 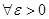 :
: 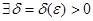 , төмендегі теңдік орынды болса:
, төмендегі теңдік орынды болса:
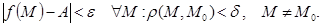
Мысал 1. Дәлелде:
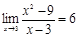 .
.
Бұл 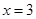 нүктесінде анықталмаған бір айнымалы функция және
нүктесінде анықталмаған бір айнымалы функция және 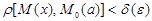
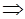
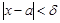 .
. 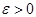 болсын. Онда
болсын. Онда 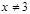 үшін
үшін 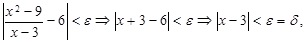
яғни, 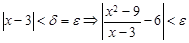 .
.
2. (тізбектер тілінде).  саны
саны  функциясының
функциясының  нүктесіндегі шегі деп аталады, егер
нүктесіндегі шегі деп аталады, егер 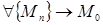 , мұндағы
, мұндағы 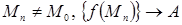 .
.
2-ші анықтамада тізбектер шегі ұғымынан функцияның шегі ұғымы шығады. 1-ші анықтама мен 2-ші анықтама эквивалентті. Дербес жағдайда, 1-ші анықтамадан 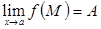 екендігі шығады, егер
екендігі шығады, егер 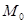 нүктесінің маңайында
нүктесінің маңайында 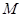 нүктелер жиыны қоюлана түссе, онда
нүктелер жиыны қоюлана түссе, онда 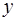 -тің сәйкес мәндері
-тің сәйкес мәндері 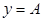 мәнінің маңайында қоюлана түседі.
мәнінің маңайында қоюлана түседі.
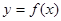 бір айнымалы функция шектерінің қасиеттерін қарастырайық.
бір айнымалы функция шектерінің қасиеттерін қарастырайық.
3. Шексіз алыстатылған нүктелердің аймағының ішіндегі мынадай 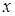 нүктелер жиынын азайта аламыз:
нүктелер жиынын азайта аламыз: 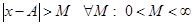 .
.
4. 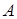 санын
санын 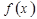 функциясының
функциясының 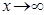 ұмтылғандағы шегі деп айтамыз, егер
ұмтылғандағы шегі деп айтамыз, егер 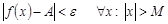 теңсіздігі орындалатындай
теңсіздігі орындалатындай 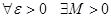 .
.
Ары қарай, 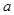 ақырлы да, шексіз де болуы мүмкін.
ақырлы да, шексіз де болуы мүмкін.
5. 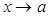 ұмтылғанда
ұмтылғанда 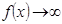 деп айтамыз, егер
деп айтамыз, егер 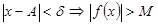 теңсіздігі орындалатындай
теңсіздігі орындалатындай 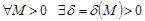 .
.
6. 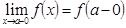 өрнегін
өрнегін 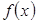 функциясының
функциясының 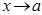 ұмтылғандағы сол жақ шегі [
ұмтылғандағы сол жақ шегі [ 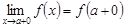 ] оң жақ шегі] деп айтамыз., егер
] оң жақ шегі] деп айтамыз., егер 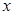 айнымалысы
айнымалысы 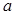 -ға ұмтыла отырып, әр уақытта
-ға ұмтыла отырып, әр уақытта 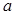 -дан кіші (үлкен) болып отырса.
-дан кіші (үлкен) болып отырса.
Егер 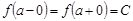 теңдігі орындалса,
теңдігі орындалса, 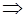
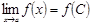 орынды екені анық.
орынды екені анық.
1.1 Шектердің қасиеттері
1. 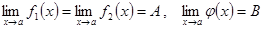 болсын және
болсын және  нүктесінің қандай да бір аймағында
нүктесінің қандай да бір аймағында
а) 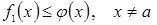 . Онда
. Онда 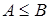 .
.
б) 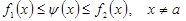 . Онда
. Онда 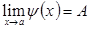 .
.
2. Тұрақтының шегі осы тұрақтының өзіне тең.
3. Егер 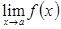 және
және 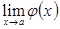 шектері ақырлы болса, онда:
шектері ақырлы болса, онда:
а) 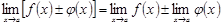 ,
,
б) 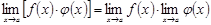
в) Егер 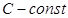 , онда
, онда 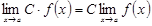 ,
,
г) 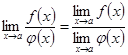 , егер
, егер 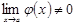 .
.
Ескерту 1. Жоғарыда көрсетілген функцияның шектерінің қасиеттері тізбектің шектері үшін де орынды.
3.2. Шексіз кіші және шексіз үлкен функциялар
Анықтама 7. 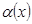 функциясы
функциясы 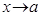 ұмтылғанда шексіз кіші (үлкен) деп аталады, егер
ұмтылғанда шексіз кіші (үлкен) деп аталады, егер 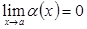
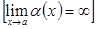 .
.
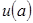 -
- 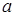 нүктесінің қандай да бір аймағы болсын,
нүктесінің қандай да бір аймағы болсын, 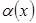 -
- 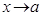 ұмтылғандағы шексіз кіші, ал
ұмтылғандағы шексіз кіші, ал 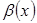 - шексіз үлкен функциялар болсын.
- шексіз үлкен функциялар болсын.
 2015-06-04
2015-06-04 7750
7750








