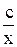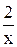Определение. Дифференциальное уравнение вида
М (х) dх + N (y) dу = 0 (1)
называется уравнением с разделёнными переменными.
Решение. Из (1) следует: M (x) dx = - N (y) dy
В левой части этого уравнения стоит дифференциал функции от x, а в правой части дифференциал функции от y. Из равенства этих дифференциалов заключаем, что сами функции могут отличаться друг от друга лишь произвольным постоянным слагаемым.
Поэтому 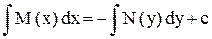 - общее решение данного уравнения.
- общее решение данного уравнения.
Пример. Найти общее решение уравнения:
x × dx + y2dy = 0
Решение. 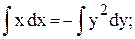
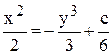
3x2 + 2y3 = c Þ y = 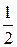
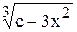 - общее решение данного уравнения.
- общее решение данного уравнения.
Определение. Уравнение вида:
MI (x) N1 (y) dx + M2(x) N2 (y) dy = 0 (2)
называется уравнением с разделяющимися переменными.
Решение. Уравнение (2) может быть приведено к уравнению (1) с разделёнными переменными путём деления обеих частей его на выражение N1 (y) M2 (x):
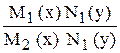 dx +
dx + 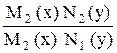 dy = 0
dy = 0
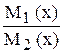 dx +
dx + 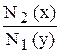 dy = 0, т.е. к уравнению (1), решать которое мы уже умеем.
dy = 0, т.е. к уравнению (1), решать которое мы уже умеем.
Замечание. Уравнение с разделяющимися переменными может быть записано в виде, разрешённом относительно y'. Тогда оно имеет вид:
y' = p (x) × q (y)
Действительно, разделив уравнение (2) на M2 (x) N2 (y) dx, получим:
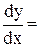
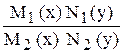 или y' = -
или y' = - 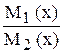 ×
× 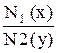
Обозначив, p (x) = - 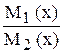 , q (y) =
, q (y) = 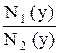 ,
,
получим y' = p (x) q (y)
Пример. Найти частное решение уравнения, удовлетворяющее начальному условию: xy' + y = 0, y 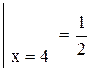
Решение. x 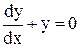 или xdy + ydx = 0
или xdy + ydx = 0 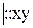
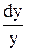 +
+ 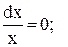
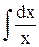 = -
= - 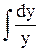 ; ln
; ln 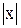 = - ln
= - ln 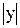 + ln
+ ln 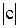 ;
;
ln 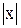 = ln
= ln 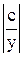 Þ x =
Þ x = 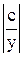 Þ
Þ
|
- общее решение данного уравнения.
Чтобы найти произвольную постоянную C, подставим начальное условие: 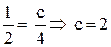
Найденное C подставим в общее решение и получим:
|
-частное решение данного уравнения, удовлетворяющее данному начальному условию.
Итак, для решения уравнения с разделяющимися переменными его необходимо преобразовать в уравнение с разделенными переменными.
 2015-06-04
2015-06-04 864
864