Определение. Функция f (x, y) называется однородной n –ого измерения относительно переменных x и y, если при любом l справедливо тождество: f (lx; ly) = lк f(x; y)
Пример. 1) Функция f (x, y) = 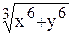 - однородная функция второго измерения.
- однородная функция второго измерения.
Действительно, f (lx; ly) = 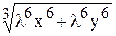 =
= 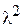
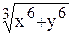 = l2 f (x, y). Итак, f (lx; ly) = l2 f (x, y); n = 2
= l2 f (x, y). Итак, f (lx; ly) = l2 f (x, y); n = 2
2)Функция f (x, y) = 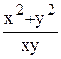 - однородная функция нулевого измерения.
- однородная функция нулевого измерения.
Действительно, f (lx; ly) = 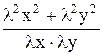 =
= 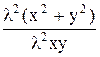 =
= 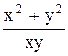 =
=
= f(x,y), т.е. f (lx; ly) = f (x, y); n = 0
Определение. Уравнение первого порядка y' = f (x, y) (3) называется однородным, если функция f (x, y) есть однородная функция нулевого измерения относительно x и y.
Решение. По условию f (lx; ly) = f (x, y).
Положив в этом тождестве l = 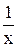 , получим f (x, y) = f (1;
, получим f (x, y) = f (1; 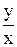 ), т.е. однородная функция нулевого измерения зависит только от отношения аргументов. Уравнение (3) примет вид:
), т.е. однородная функция нулевого измерения зависит только от отношения аргументов. Уравнение (3) примет вид:
y' = f (1; 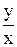 ), (4).
), (4).
Сделаем подстановку: u = 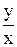 , т.е. y = ux.
, т.е. y = ux.
Тогда y' = xu' + u, и уравнение (4) примет вид:
u' x + u = f (1; u).
Это уравнение с разделяющими переменными.
x 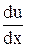 = f (1; u) – u или
= f (1; u) – u или 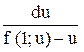 =
= 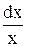
Интегрируя, найдём: 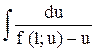 =
= 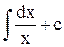 .
.
Обозначим F (u) = 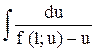 .
.
Предыдущее равенство тогда перепишется так:
F (u) = ln 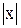 + C
+ C
Подставим вместо u отношение 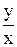 , получим интеграл уравнения (3):
, получим интеграл уравнения (3):
F (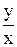 ) = ln
) = ln 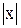 + C
+ C
Пример. Найти общее решение уравнения:
y¢ = 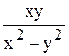 ; f (x, y) =
; f (x, y) = 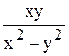 - однородная функция нулевого измерения относительно x и y. Сделаем подстановку
- однородная функция нулевого измерения относительно x и y. Сделаем подстановку 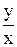 = u, т.е. y = ux. Тогда
= u, т.е. y = ux. Тогда
y¢ = x 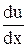 + u; x
+ u; x 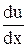 + u =
+ u = 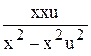
x 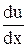 + u =
+ u = 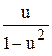 ; x
; x 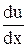 =
= 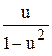 - u; x
- u; x 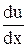 =
= 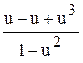 ;
;
x 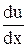 =
= 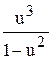 ; x (1 – u2) du = u3 dxô: u3 x
; x (1 – u2) du = u3 dxô: u3 x
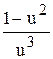 du =
du = 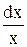
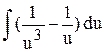 =
= 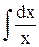 .
.
Интегрируя, находим:
- 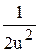 - ln
- ln 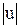 = ln
= ln 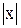 + ln
+ ln 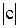 ; -
; - 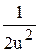 = ln
= ln 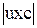
Подставляя u = 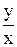 , получим общий интеграл исходного уравнения.
, получим общий интеграл исходного уравнения.
- 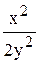 = ln
= ln 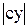 ; x2 = -2y2 ln
; x2 = -2y2 ln 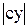 ; y2 = -
; y2 = -  ; y =
; y = 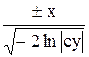
- общее решение.
Замечание. Уравнение M (x, y) dx + N (x, y) dy = 0 (5) будет однородным в том случае, когда M (x, y), N (x, y) являются однородными функциями одного и того же измерения. Это вытекает из того, что отношение двух однородных функций одного и того же измерения является однородной функцией нулевого измерения.
Пусть M (x, y), N (x, y) – однородные функции одного и того же измерения n, т.е. M (lx; ly) = ln M (x, y); N (lx, ly) = ln N (x, y).
Тогда, разделив обе части уравнения (5) на N (x, y) dx, получим:
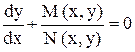 ;
; 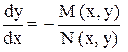
т.е. y¢ = f (x, y), где f (x, y) = - 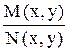 - однородная функция нулевого измерения, так как
- однородная функция нулевого измерения, так как
f (lx; ly) = - 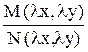 = -
= - 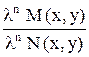 = -
= - 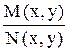 = f (x, y).
= f (x, y).
Пример. Найти общее решение уравнения (x2 + y2) dx – 2xy dy = 0
Данное уравнение однородное. Функции M (x, y) = x2 + y2; N (x, y) = - 2xy – однородные функции второго измерения. Найдём общее решение этого уравнения.
Данное уравнение разделим на 2xy dx и получим:
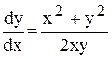 ,
, 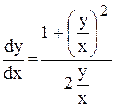
Сделаем подстановку u= 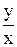 , т.е. y = ux, тогда
, т.е. y = ux, тогда
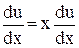 + u.
+ u.
Подставим всё это в уравнение:
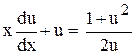 ;
; 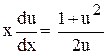 - u;
- u; 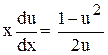
Делим переменные:
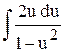 =
= 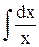 Þ - ln
Þ - ln 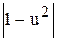 = ln
= ln 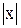 + ln
+ ln 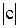 ;
;
ln 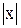 + ln
+ ln 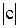 + ln
+ ln 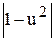 = 0; ln
= 0; ln 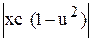 = 0
= 0
xc (1 – u2) = 1; xc (1 - 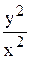 ) = 1;
) = 1;
c (x2 – y2) = x; cx2 - cy2 = x; cx2 – x = cy2.
y = ± 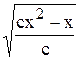 - общее решение данного уравнения.
- общее решение данного уравнения.
Итак, для решения однородных дифференциальных уравнений необходимо произвести подстановку и преобразовать это уравнение к уравнению с разделяющимися переменными.
 2015-06-04
2015-06-04 5768
5768
