2015-06-05
762
Для сгруппированной, то есть разделенной на группы, статистической совокупности можно вычислить три вида дисперсии: общая, внутригрупповая и межгрупповая.
Для оценки непрерывного признака внутри группы рассчитывается внутригрупповая дисперсия:
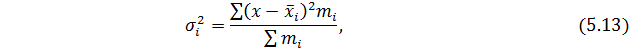
где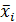 
– среднее значение признака в i -ой группе.
Далее рассчитывается среднее значение из групповых дисперсий:
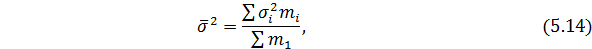
Межгрупповая дисперсия показывает вариацию групповых средних вокруг средней величины признака в совокупности:
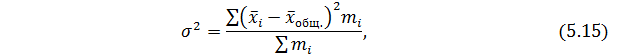
Общая дисперсия определятся по правилу сложения дисперсий, а ее значение таково:
Общая вариация признака в совокупности складывается из вариации признака внутри отдельных групп и вариации между группами:
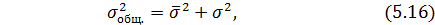
Пример 3. Имеются данные о результатах сдачи экзамена по двум группам на курсе.
Таблица 5.3
| Оценки | Количество студентов в 1-ой группе | Количество студентов во 2-ой группе |
| Итого |
Решение: Определяется средняя оценка в каждой группе:
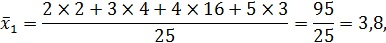
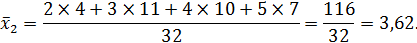
Рассчитывается общая средняя:
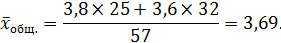
Находится дисперсия в каждой группе:
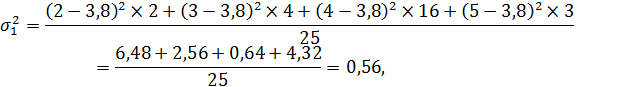
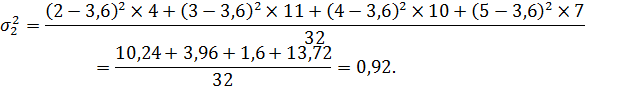
Далее определяется средняя дисперсия по двум группам:
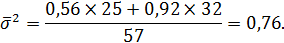
Рассчитывается межгрупповая дисперсия:
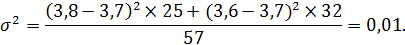
Общая дисперсия составит:
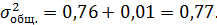
Среднее квадратическое отклонение будет равно:
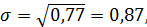
это означает, что оценка каждого студента в каждой группе отклоняется от средней на 0,87.
1. Что такое вариация и каковы этапы ее статистического анализа?
2. Какими показателями характеризуется центр распределения?
3. Как соотносятся между собой средняя и мода в симметричном распределении; в левосторонней асимметрии; в правосторонней асимметрии.
4. С помощью каких показателей определяется степень вариации?
5. Какой показатель характеризует степень однородности совокупности?
6. Что характеризует эксцесс распределения?
7. В чем состоит правило сложения дисперсий?
