2015-06-05
9796
Асимметрия и эксцесс являютсяхарактеристиками формы распределения.
В практике статистического исследования приходится встречаться с различными распределениями. Идеальным (нормальным) распределением является такое, у которого распределение признака в совокупности симметричное, при этом мода и средняя совпадают.
Однако чаще всего встречается асимметрическое распределение. При правосторонней асимметрии, средняя арифметическая больше моды, а при левосторонней, наоборот.
Для оценки степени асимметричности применяют моментный и структурный коэффициент асимметрии.
Моментный коэффициент асимметрии определяется по формуле:
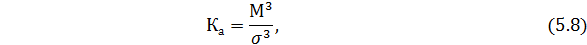
где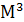 
- центральный момент третьего порядка. Определяется по
формуле:
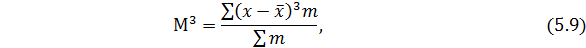
Структурные показатели асимметрии характеризуют асимметричность только в центральной части распределения, т.е. основной массы единиц.
Наиболее часто применяют структурный коэффициент асимметрии, который определяется по формуле:
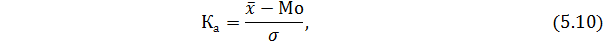
Если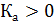 
, асимметрия правосторонняя, если 
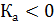, асимметрия левосторонняя.
Формы распределения признаков в совокупности приведены на рис. 5.4.
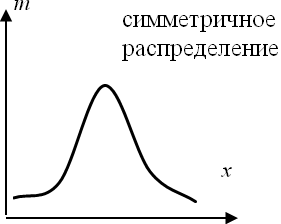
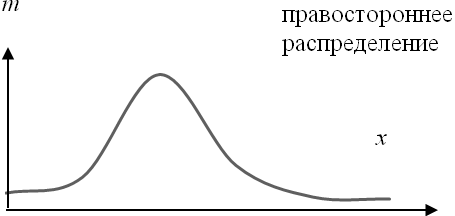
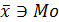
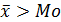
| левостороннее распределение |
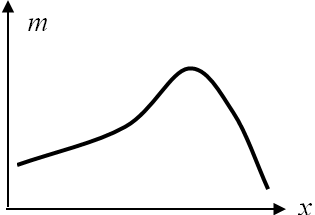
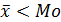
Рис. 5.4. Формы распределения признаков в совокупности
Другим свойством рядов распределения является эксцесс. Под эксцессом понимают островершинность или плосковершиннсоть распределения по сравнению с нормальным распределением, т. е. эксцесс – это отклонение вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения.
Эксцесс оценивается с помощью показателя, представлено формулой:
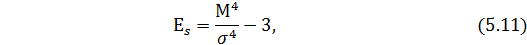
где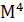 
- центральный момент 4-го порядка, который определяется по
формуле:
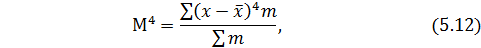
Распределение островершинное обладает положительным эксцессом (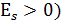
, а плосковершинное – отрицательным эксцессом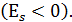 
На рис. 5.5 представлено нормальное, островершинное и плосковершинное распределение.
| m |
| m |
| x |
| x |
2 – островершинное распределение
3 – плосковершинное распределение
Рис. 5.5. Формы распределения вариационного ряда
Пример 2. Для определения средней продолжительности представленных междугородних разговоров проведено выборочное наблюдение, в выборку попало 340 разговоров. Распределение этих разговоров по продолжительности представлено в виде вариационного ряда в таблице 5.1. Определить основные характеристики вариационного ряда. Ряд изобразить графически в виде гистограммы.
Таблица 5.2
| Группа телефон-ных разговоров по продол- житель-ности (мин.) | Коли- чество разгово- ров m | Середина интервала x | xm | Накоплен- ные частоты |  |  |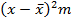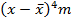
| До 3 3-5 5-7 7-9 9-11 11-13 Более 13 | 921,6 352,8 65,28 112,3 419,8 540,8 725,7 | 212,33 41,8 161,7 | ||||
| Итого | 80745,9 |
Решение:
1. Определяется средняя продолжительность междугородних разговоров:
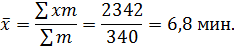
2. Рассчитывается мода, при этом модальный интервал 5-7:
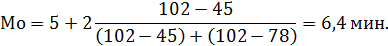
Это означает, что большинство разговоров имеет продолжительность 6,4 мин.
3. Определяется медиана, для этого определяются накопленные частоты.
Сначала находится следующее соотношение:
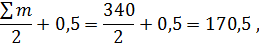
Сравнивая его с накопленными частотами, можно сказать, медиальный интервал будет равен 5-7 мин.
Медиана равна:
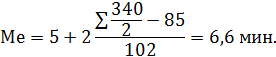
Таким образом, половина разговоров имеет продолжительность до 6,6 мин., а половина больше.
4. Размах колебаний будет равен:
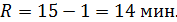
при этом первый и последний интервал закрываются.
5. Среднее квадратическое отклонение составит:
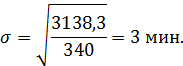
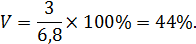
В среднем продолжительность каждого разговора отклоняется от среднего значения на 3 мин. или на 44%. Совокупность не однородная, так как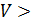 
33%, а средняя не типична для данной совокупности.
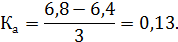
Так как 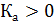, это означает, что распределения имеют форму правосторонней асимметрии.
Рассчитывается эксцесс, но сначала определяется момент 4-го порядка:
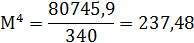
9. Эксцесс будет равен:
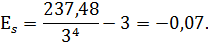
Это означает, что распределение плосковершинное. Графическое изображение ряда представлено на рис. 5.6.
| m |
| Мо |
| x |
Рис. 5.6. Гистограмма распределения телефонных разговоров по продолжительности
