Системы координат применяемые в геодезии

Координаты – это совокупность чисел определяющих положение любой точки на поверхности или в пространстве относительно выбранной системы.

Например:

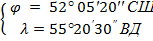- геодезические координатные точки

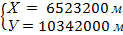- прямоугольные координаты точки

Из приведенного примера видно, что в инженерной геодезии применяются две основных системы координат:

- геодезическая система координат,

- плоская прямоугольная система координат.

Геодезическая СК

В этой системе за координатную поверхность принимается поверхность эллипсоида, а за основные координатные линии – геодезические меридианы и параллели.

Меридиан – это линия пересечения поверхности эллипсоида плоскостью проходящей через ось вращения.

Параллель – это линия пересечения поверхности эллипсоида плоскостью проходящей перпендикулярно оси вращения. Параллель, проходящая через центр эллипсоида, называется экватором.

Меридиан задается геодезической долготой точки, параллель – геодезической широтой.

Геодезической широтой φ точки называется угол между нормалью к поверхности эллипсоида в данной точке и плоскостью экватора.

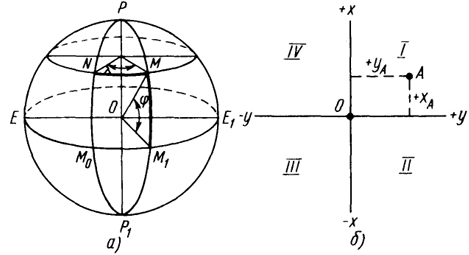
Рисунок 2 - Системы географических (а) и плоских прямоугольных (б) координат

Широты измеряются от плоскости экватора к северу и к югу от 0° до 90°.

Например:

φ = 20°25'30'' с.ш.( или ю.ш.).

Геодезической долготой λ точки называется двугранный угол между плоскостью геодезического меридиана данной точки и плоскостью нулевого меридиана, за который принят меридиан Гринвича. Долгота измеряется от плоскости нулевого меридиана к востоку (в.д.) и к западу (з.д.) от 0° до 180°.

Третьей координатой каждой точки физической поверхности Земли является ее высота над поверхностью земного эллипсоида (абсолютная высота). В России абсолютные высоты отмеряются от уровня Балтийского моря. Уровень моря измеряется специально установленной линейкой называемой футшток. Футшток установлен на устое Синего моста через Обводный канал в Кронштадте. От нуля Кронштадтского футштока на всей территории бывшего Советского Союза производятся измерения абсолютных высот.

С 1898 г. в Кронштадте работает автоматический самопишущий прибор - мареограф, фиксирующий изменения уровня моря. Сначала он располагался в деревянной будке, затем в специальном павильоне. Павильон футштока - маленькая башенка в стиле петровской архитектуры - поставлен над колодцем глубиной 7 м, который сообщается с Финским заливом. В колодце на поверхности воды лежит специальный поплавок, соединенный с самопишущим прибором. Мареограф непрерывно рисует кривую уровня Балтийского моря. Средняя величина уровня приведена к нулю Кронштадтского футштока.

Рисунок 3 - Здание мареографа

Плоская прямоугольная система координат.

Прежде, чем рассматривать вопрос о прямоугольных координатах, поговорим о картографической равноугольной проекции (конформной проекции).

Чтобы установить связь между геодезическими координатами любой точки на сфероиде и прямоугольными геодезическими координатами той же точки на плоскости, применяют особый способ проектирования всего земного сфероида на проектирующую плоскость по частям, или по так называемым зонам. Для этого весь земной шар разделяют меридианами на шести- или трехградусные зоны, простирающиеся от северного полюса к южному (рисунок 4).

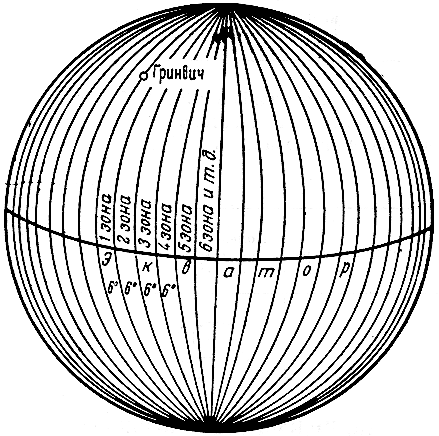
Рисунок 4

В итоге получаем 60 зон. Счет зон ведется на восток от нулевого меридиана. Каждую зону проектируют на плоскость отдельно при помощи цилиндра. Перенос изображения местности со сферической поверхности каждой зоны на цилиндрическую выполняется под условием сохранения равенства углов на сфере и на цилиндре. Закончив последовательное проектирование поверхности всех зон, цилиндр развертывают на плоскости. В результате получают изображение каждой зоны в проекции на плоскость. Такая проекция называется равноугольной или конформной. Эта проекция так же называется проекцией Гаусса. Иногда ее называют проекцией Гаусса - Крюгера.

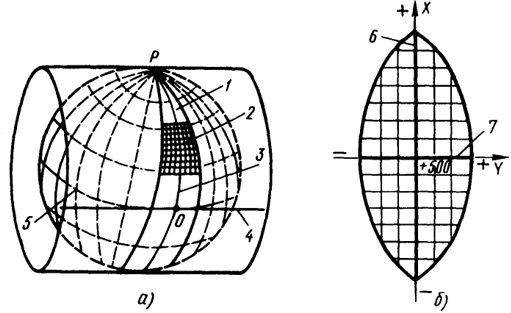
Рисунок 5 - Поперечно- цилиндрическая проекция Гаусса-Крюгера (а)

и зональная система координат (б):
1 - зона, 2 - координатная сетка, 3 - осевой меридиан, 4 - ось Y, 5 - экватор, 6 - проекция осевого меридиана, 7 - проекция экватора

В ней теоретическая разработка проекции принадлежит Гауссу; Крюгер детально разработал формулы для ее применения в геодезии. Каждая зона такой проекции на плоскости изображается таким образом, чтобы осевой меридиан зоны изображался прямой линией, второй прямой перпендикулярной осевому меридиану, является линия экватора. Показанные на рисунке линии, параллельные изображению осевого меридиана и экватора, образуют прямоугольную координатную сетку (рисунок 5,б).

Для точки А прямоугольные геодезические координаты будут:

Ха – расстояние от экватора в метрах.

Уа – расстояние от осевого меридиана в метрах.

Для того, чтобы исключить отрицательные значения по оси У, осевой меридиан считают не за ноль, а за 500 км. Тогда если Уа меньше 500 км, то точка находится слева от осевого меридиана и наоборот. Прямоугольные координаты записываются так:

Ха = 6065700 м – расстояние от экватора в м.

Yа = 10.384.060 м.

Необходимо отметить, что в координате Y_а число 10 – номер зоны (номер зоны всегда занимает место, соответствующее в общем числе цифрам тысяч километров или миллионов метров, если координата У выражена в метрах). Например: У = 10384 км, здесь число 10 соответствует тысячам километров, значит точка с указанными координатами находится в 10 зоне.

Если координата У выражена в метрах, например У = 10 384 060 м, здесь число 10 соответствует миллионам метров, значит точка с указанными координатами также находится в 10 зоне.