1.1. Исходные данные
Плановое обоснование для разбивки на местности опор мостового перехода выполнено методом геодезического четырехугольника, схема которого представлена на рис. 1. Опорные точки 5, 6, 11 и 12 закреплены на местности по типу временных геодезических знаков в виде столиков для установки теодолита. На каждой точке измерены углы электронным теодолитом 3Та5р, значения которых указаны на рис. 1. Среднеквадратическая погрешность измерения одного угла (паспортная точность теодолита) составляет m = ± 5". На этом же рис.1 в кружках обозначены номера углов № 1,2,3,4,5,6,7,8, в квадратиках номера треугольников № 1, 2, 3, и стороны буквами A,B,C,D,E,F. Для определения допуска на угловую погрешность устанавливается коэффициент значимости t = 1,96 ≈ 2,0, который ограничивает величину фактической погрешности измерений в 95%.
Дирекционный угол линии 5-6 (α56), длина линии A (d 56) и координаты опорной точки 6 (X6, Y6). принимаются каждым студентом индивидуально по номеру варианта (табл. 1), назначаемому преподавателем.
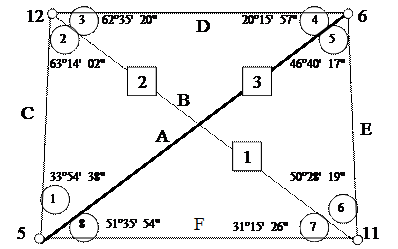 |
Рис. 1 Схема геодезического четырехугольника
1.2. Уравнивание углов, вычисление сторон и координат
Уравнивание углов (табл. 2), вычисление сторон (табл. 3) и координат (табл. 4) геодезического четырехугольника выполнить в стандартных ведомостях.
Уравнивание углов. В соответствии с исходными данными (см. рис. 1) в ведомость уравнивания углов (см. табл. 2, колонка 2) выписать углы измеренные. При этом использовать нумерацию углов рис. 1 и соответствующую нумерацию углов в табл. 2 (колонка 1).
Вычислить сумму восьми измеренных углов (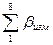 ) и фактическую угловую невязку δф по условию полигона. Оценить точность угловых измерений, сопоставив фактическую и допустимую (δдоп) угловые невязки. При этом использовать следующие формулы:
) и фактическую угловую невязку δф по условию полигона. Оценить точность угловых измерений, сопоставив фактическую и допустимую (δдоп) угловые невязки. При этом использовать следующие формулы:
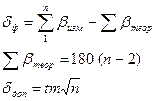 (1)
(1)
где n – количество измеренных углов;
t – коэффициент значимости (см. выше “исходные данные”);
m – паспортная точность теодолита, используемого для измерения углов, (см. выше “исходные данные”).
Если δф ≤ δдоп, то продолжить вычисления.
Вычислить суммы углов (см. рис. 1)
β1+β2; β5+β6; β3+β4; β7+β8.
Вычислить невязки f1 и f2 по формулам:
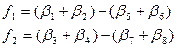 . (2)
. (2)
По данным вычисления невязок f1 и f2 выполнить оценку точности измерения углов, используя формулы (1). Если каждая невязка f1 и f2 меньше или равна соответствующей допустимой невязке, то продолжить вычисления.
Вычислить поправки в углы по формулам:
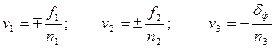 . (3)
. (3)
где n1, n2 и n3 – количество углов использованных при вычислении соответствующей невязки f1, f2 и δф.
Причем, поправки v1 в углы β1, β2 принять со знаком минус, в углы β5, β6 – со знаком плюс, и поправки v2 в углы β3, β4 – со знаком плюс, в углы β7, β8 – со знаком минус. Поправки v3 во все углы принять со знаком противоположным знаку невязки δф.
Таблица 2
Уравнивание углов
| № угла | Углы измеренные, β ° ' " | Суммы (1+2) (5+6) (3+4) (7+8) | Невязки f1= β (1+2) - β (5+6) f2= β (3+4) - β (7+8) | Поправки | Углы уравновншенные β ° ' " | № угла | ||
| По условиям β (1+2) = β (5+6) β (3+4) = β (7+8). ± f1/ 4 ± f2/ 4 | По условию ∑ β (1-8) = ∑ β т - δ /8 | Суммарные поправки, v∑ | ||||||
| 33 54 38 | 97 08 40 | f1 = 97 08 40 - 97 08 36 = + 0 00 04 | -1,0 | +0,875 | -0,125 | 33 54 37,9 | ||
| 63 14 02 | -1,0 | +0,875 | -0,125 | 63 14 01,9 | ||||
| 46 40 17 | 97 08 36 | +1,0 | +0,875 | +1,875 | 46 40 18,9 | |||
| 50 28 19 | +1,0 | +0,875 | +1,875 | 50 28 20,9 | ||||
f1(доп) =±mt 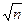 =±2*2 =±2*2 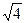 = ±8" = ±8" | ∑ 0,0 | ∑ +3,500 | β (1+2) = 97 08 39,8 β (5+6) = 97 08 39,8 | |||||
| 62 35 20 | 82 51 17 | f2 = 82 51 17 -82 51 20 = - 0 00 03 | +0,75 | +0,875 | +1,625 | 62 35 21,6 | ||
| 20 15 57 | +0,75 | +0,875 | +1,625 | 20 15 58,6 | ||||
| 31 15 26 | 82 51 20 | -0,75 | +0,875 | +0,125 | 31 15 26,1 | |||
| 51 35 54 | -0,75 | +0,875 | +0,125 | 51 35 54,1 | ||||
f2(доп) =±mt 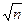 =±2*2 =±2*2 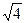 = ±8" = ±8" | ∑ 0,00 | ∑ +7,000 | ∑ +3,500 | β (3+4) = 83 51 20,2 β (7+8) = 83 51 20,2 | ||||
| ∑ β (1-8) | 359 59 53 | ∑ +7,000 | ∑ β (1-8)=360 00 00 | |||||
δф = ∑ β (1-8) - ∑ β т δф =359 59 53–360 00 00 = - 0 00 07 δдоп = ± m t 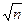 = ±2*2 = ±2*2 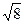 = ± 11,3" = ± 11,3" |
Таблица 3
Вычисление сторон (решение треугольников)
| № треу-голь-ника | № точки | № угла | Уравновешенные углы, β ° ' " | Sin углов Sin β | Вычисленная длина сторон, d, м | Поправки в длины сторон, м | Исправлен-ная длина сторон, d, м | Обозначение сторон |
| 6+7 | 81 43 47,0 | 0,98960054 | 492,480 | 492,480 | А | |||
| 51 35 54,1 | 0,78367569 | 390,000 | 0,000 | 390,000 | E | |||
| 46 40 18,9 | 0,72743652 | 362,013 | 0,000 | 362,013 | F | |||
| 180 00 00,0 | ||||||||
| 2+3 | 125 49 23,5 | 0,81082695 | 492,480 | 0,000 | 492,480 | A | ||
| 20 15 58,6 | 0,34638358 | 210,386 | 0,000 | 210,386 | C | |||
| 33 54 37,9 | 0,55789761 | 338,856 | +0,001 | 338,857 | D | |||
| 180 00 00,0 | ||||||||
| 50 28 20,9 | 0,77131889 | 338,856 | +0,001 | 338,857 | D | |||
| 4+5 | 66 56 17,5 | 0,92008283 | 404,211 | +0,001 | 404,212 | B | ||
| 62 35 21,6 | 0,88772970 | 389,998 | +0,002 | 390,000 | E | |||
| 180 00 00,0 |
fd = E3 – E1 = 389,998 - 390,000 = -0,002 м
vE = - fd = +0.002; vD = vB = 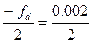 = +0,001 м
= +0,001 м
Таблица 4
Ведомость вычисления координат точек опорной сети
| № то-чек | Углы исправ-ленные ° ' " | Дирек-ционные углы ° ' " | Исправ-ленные стороны d, м | Вычисленные прирашения координат, м | Поправки, м | Исправленные приращения координат, м | Координаты, м | № то-чек | ||||
| ∆X | ∆Y | δX | δY | ∆X | ∆Y | X | Y | |||||
| прав | ||||||||||||
| 21 55 18,0 | ||||||||||||
| 46 40 18,9 | 2954,980 | 5068,740 | ||||||||||
| 155 14 59,1 | 390,000 | -354,175 | 163,279 | -354,175 | 163,279 | |||||||
| 50 28 20,9 | 2600,805 | 5232,019 | ||||||||||
| 284 46 38,2 | 404,212 | 103,099 | -390,842 | +0,001 | 103,100 | -390,842 | ||||||
| 296 45 58,1 | 2703,905 | 4841,177 | ||||||||||
| 168 00 40,1 | 210,386 | -205,797 | 43,702 | -205,797 | 43,702 | |||||||
| 326 05 22,1 | 2498,108 | 4884,879 | ||||||||||
| 21 55 18,0 | 492,480 | 456,871 | 183,862 | +0,001 | -0,001 | 456,872 | 183,861 | |||||
| 2954,980 | 5068,740 | |||||||||||
| ∑ β | 720 00 00,0 | ∑ d =1497,078 | ∑∆X= -0,002 | ∑∆Y= + 0,001 | ∑ δX= + 0,002 | ∑δY= -0,001 | ∑∆X = 0,000 | ∑∆Y= 0,000 | ||||
| ∑ β т | 720 00 00,0 | fx = - 0.002 | fy = +0.001 | |||||||||
| f (абс) = ± 0.002 | ||||||||||||
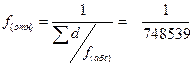 | f (отн, доп) = 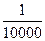 | |||||||||||
Все вычисленные поправки округлить точностью до 0,1". Учитывая знаки соответствующих поправок вычислить суммарные поправки для каждого угла v∑ = v1 + v3; v∑ = v2 + v3.
Исправить измеренные углы βиспр = βизм + v∑, при этом необходимо учитывать знаки суммарных поправок. Вычисления выполнить с точностью 0,1".
Выполнить контрольные вычисления сумм поправок и сумм углов. Данные уравновешивания углов и контрольных вычислений записать в табл. 2 в соответствующие колонки и строки (см. табл. 2).
Вычисление сторон (решение треугольников). По номерам указанным в квадратиках (см. рис. 1) определить номера треугольников и нумерацию их вершин. В соответствии с номером треугольника установить последовательность их записи в ведомость вычисления сторон (см. табл. 3). Для каждого треугольника в ведомости вычисления сторон (см. табл. 3) установить последовательность нумерации точек, которая должна начинаться с номера угла напротив известной стороны А (см. рис. 1), затем продолжаться номером угла напротив промежуточной стороны и заканчиваться номером угла напротив связующей стороны (стороны принадлежащей двум последовательным треугольникам). Из ведомости уравнивания углов (см. табл. 2) в ведомость вычисления сторон (см. табл. 3) в третью колонку выписать уравновешенные углы. Причем необходимо выписать углы в соответствии с их нумерацией указанной в колонке 2 табл. 3. В случае указанной суммы углов произвести их суммирование. Для каждого треугольника (см. рис. 1) вычислить контрольные суммы углов, которые должны быть точно равны 180°. Установить синусы всех углов треугольников с точностью до 0,000000001.
В соответствии с вариантом решения задачи (см. табл. 1) в ведомость вычисления сторон (см. табл. 3) в соответствующие строки и колонки выписать численное значение исходной стороны A (см. рис.1). В ведомости вычисления сторон (см. табл. 3) последовательно, начиная с первого треугольника, вычислить промежуточные и связующие стороны по формуле:
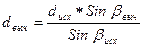 , (4)
, (4)
где dвыч – вычисляемая сторона треугольника;
dисх – исходная (известная) сторона треугольника (для первого и второго треугольника сторона А, см. рис. 1 и табл. 3);
Sin βвыч – синус угла треугольника, находящегося напротив вычисляемой стороны (см. табл. 3);
Sin βисх – синус угла треугольника, находящегося напротив известной стороны (см. табл. 3).
Вычисления по формуле (4) сторон (см. рис. 1) E и F в первом треугольнике и сторон C и D во втором треугольнике выполнить по известной исходной стороне А (см. рис. 1 и табл. 3). Вычисление сторон B и E в третьем треугольнике выполнить по стороне D, значение которой установлено из вычислений во втором треугольнике. Сопоставить численные значения стороны E установленные по вычислениям в первом (E1) и третьем (E3) треугольнике. Принять за вероятнейшее значение стороны Е, численное ее значение (E1), полученное из первого треугольника. В этом случае невязку установить по формуле:
fd = E3 – E1. (5)
Вычислить поправки для сторон E и B третьего треугольника и для стороны D третьего и второго треугольников по формулам (см. табл. 3):
vE = - fd; и vB = vD = 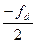 . (6)
. (6)
Вычислить исправленные стороны по формуле:
dиспр = dвыч + vd (7)
Данные вычислений записать в соответствующие графы и колонки табл. 3.
Вычисление координат. Исходными данными для вычисления координат точек опорной сети в стандартной ведомости (см. табл. 4) являются уравновешенные углы (см. табл. 2), исходный дирекционный угол (α 56), принимаемый в соответствии с вариантом решения задачи (см. табл. 1), вычисленными длинами сторон (см. табл. 3) и координатами исходной точки 6, принимаемыми в соответствии с вариантом решения задачи (см. табл. 1).
В первую очередь необходимо принять последовательность нумерации точек. Для этого можно использовать следующие варианты (см. рис.1):
5→6→12→11→5→6; (8)
5→6→11→12→5→6. (9)
В качестве примера решения задачи в настоящих методических указаниях принят вариант по последовательности (8) (см. табл. 4).
Из ведомости уравнивания углов (см. табл. 2) в ведомость вычисления координат (см. табл. 4) выписать левые по принятому варианту последовательности нумерации точек уравновешенные углы. Углы будут левыми, если мысленно встать на предыдущую точку, например 5, и повернувшись лицом по направлению последующей точки (точки 6) на этой последующей точке угол будет слева по ходу. В противном случае углы будут правыми. Например, для последовательности (8) углы будут левые, а для последовательности (9) – правые.
Проверить правильность выписки углов путем их суммирования. При этом, поскольку на двух (m = 2) точках 11 и 5 необходимо вычислять левые по ходу углы, как дополнения до 360°, то теоретическая сумма углов будет равна:
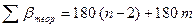 . (10)
. (10)
По принятому варианту решения задачи из табл. 1 в ведомость вычисления координат выписать исходный дирекционный угол (α 56), который записать в соответствующие строки колонки 3 (см. табл. 4).
Вычислить дирекционные углы остальных линий хода по формуле:
для левых углов, принятых по последовательности точек (8)
αпосл = αпред + βлев - 180°; (11)
или для правых углов, если принята последовательность точек (9)
αпосл = αпред + 180° - βправ. (12)
Если при вычислении по формуле (11) αпред + βлев < 180°, то использовать формулу: αпосл = αпред + βлев + 360° - 180°;
и если αпред + βлев - 180° > 360°, то αпосл = αпред + βлев - 180° - 360°.
Если при вычислении по формуле (12) αпред + 180° < βправ, то использовать формулу: αпосл = αпред + 180° + 360° - βправ;
и если αпред + 180° - βправ > 360°, то αпосл = αпред + 180° - βправ - 360°.
Контролем правильности вычисления дирекционных углов служит критерий точного равенства вычисленного дирекционного угла α 56, при последовательном вычислении по формулам (11) или (12) и того же угла, записанного как исходного для линии 5-6 в нижней строке третьей колонки табл. 4.
Из ведомости вычисления сторон (см. табл. 3.) в ведомость вычисления координат (см. табл. 4, колонка 4) по принятой последовательности вычислений (8) или (9) выписать соответствующие стороны. Вычислить приращения координат по формулам:
∆Xi = di Cos αi; (13)
∆Yi = di Sin αi. (14)
Подсчитать в соответствующих колонках табл.4
∑ di; ∑ ∆Xi; ∑ ∆Yi
и вычислить невязки по осям координат:
fx = ∑ ∆Xi - ∑ ∆XТ; (15)
fy = ∑ ∆Yi - ∑ ∆YТ, (16)
где ∑ ∆XТ = ∑ ∆YТ = 0.
Вычислить абсолютную погрешность:
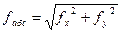 (17)
(17)
и, наконец, относительную погрешность, которая должна удовлетворять неравенству
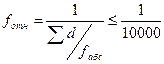 . (18)
. (18)
В случае выполнения неравенства (18) можно продолжить вычисления. В противном случае проверить правильность выписки сторон из ведомости их вычисления или правильность вычислений по формулам (13), (14) или вычисления сумм ∑ di; ∑ ∆Xi; ∑ ∆Yi, а также вычисления по формулам (15), (16), (17) и (18).
Определить поправки в приращения координат vx и vy с точностью 0,001 метра. При этом необходимо использовать следующие принципы: знаки поправок должны быть обратными по отношению к знаку невязок, вычисленных по формулам (15), (16); большие численные значения поправок vx и vy должны соответствовать большим численным значениям сторон (d) полигона; сумма поправок ∑ vx или ∑ vy должна быть равна с обратным знаком соответствующим невязкам fx или fy. Если быть точным, то поправки необходимо вычислять по формулам:
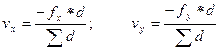 , (19)
, (19)
при точном выполнении условий
∑ vx = - fx; ∑ vy = - fy. (20)
Однако вычисления по формулам (19) небольших численных значений невязок приводят к поправкам, которые могут иметь значащую цифру только в четвертом или пятом разряде после запятой. Такие поправки для практической цели не имеют смысла. Поэтому необходимо выдержать требование округления поправок с точностью 0,001 метра и выше сформулированные принципы. Это достигается путем введения поправок равных 0,001 м в приращения координат только для тех сторон, которые имеют большие численные значения. Для других приращений координат поправки будут равны нулю. В любом случае при определении поправок должны выполняться условия (20).
Вычислить исправленные приращения координат:
∆Xиспр = ∆Xвыч + vx; (21) ∆Yиспр = ∆Yвыч + vy. (22)
Вычислить координаты точек опорной сети:
Xпосл = Xпред + ∆Xиспр (23)
Yпосл = Yпред + ∆Yиспр (24)
Контролем вычисления координат опорной сети является следующее правило: координаты последней точки (исходной), вычисленные при использовании формул (23) или (24), должны быть точно равны координатам той же исходной точки.
 2015-06-28
2015-06-28 6116
6116
