Методические указания по изучению темы «Характеристики рассеяния

(дисперсия, среднее квадратическое отклонение,

коэффициент вариации)»

В рамках данной темы необходимо усвоить ее основные понятия, а именно: варьируемость, вариация, полный диапазон (размах вариации), промежуточный диапазон, интерквартильный диапазон, 10-90% диапазон, дисперсия, рассеяние, среднее квадратическое отклонение, коэффициент вариации.

На примере предыдущей темы студенты должны были убедиться в том, что характеристики положения, хоть и являются чрезвычайно важными при изучении варьирующего признака, все же не дают полной информации о нем. Нетрудно представить себе два эмпирических распределения, у которых средние одинаковы, но при этом у одного из них значения признака рассеяны в узком диапазоне вокруг среднего, а у другого – в широком. Поэтому наряду со средними значениями вычисляют и характеристики рассеяния выборки. В рамках данной темы рассматриваются наиболее употребляемые из них: размах вариации, дисперсия, среднее линейное и квадратическое отклонение, коэффициент вариации. Студентам необходимо запомнить определения этих характеристик и усвоить процедуры их вычисления.

Размах вариации - это интервал, заключающий в себе все значения. Можно вычислить разность между истинными крайними значениями множества переменных, которые в этом случае устанавливают границы размаха вариации. Иногда эта величина обозначается как «включающий» диапазон и определяется: 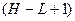; например (12 - 2) + 1.

Еще более ограниченным является промежуточный диапазон между первым и третьим квартилями (интервал, который содержит средние 50% случаев). Обычно он называется интерквартильным диапазоном. Подобная процедура обнаруживает степень группируемости случаев, относящихся к среднему интервалу, вокруг медианы.

Дисперсией называется средний квадрат отклонения значений признака от среднего арифметического. Дисперсия, вычисляемая по выборочным данным, называется выборочной дисперсией и обозначается .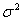

Выборочную дисперсию вычисляют по приведенным ниже формулам:

Для несгруппированных данных 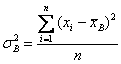. В этой формуле 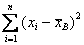– сумма квадратов отклонений значений признака x_i от среднего арифметического х. Для получения среднего квадрата отклонений эта сумма поделена на объем выборки n.

Для сгруппированных данных:

,

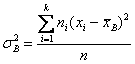где: х_i – срединные значения интервалов группировки;

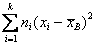– взвешенная сумма квадратов отклонений.

Стандартное или среднее квадратическое отклонение (сигма) обозначается с помощью греческой буквы 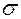и вычисляется путем нахождения корня квадратного из дисперсии по формуле: .

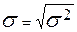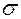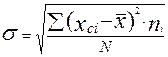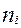Для получения сгруппированных данных применяется формула: , где - частота, 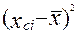- отклонение средней точки интервала от среднего арифметического.

Стандартное отклонение может быть превращено в меру относительной вариации посредством нормирования его по отношению к собственному началу отсчета (то есть среднему арифметическому), которая называется коэффициентом вариации и вычисляется по формуле .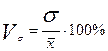

Студентам следует запомнить, что малое значение 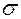при большом среднем указывает на большую однородность данных и в силу этого на типичность среднего, что в некоторых условиях крайне существенно.

Вариацию качественных переменных нельзя измерять тем же способом, который был разработан для количественных. Вместо вычисления величин подсчитываются различия в качествах.

Любое событие исследователь рассматривает не изолированно, а в сравнении с конкретной нормой, вытекающей из социальной основы данного события. Совокупность процедур можно назвать операциями нормировки, поскольку они устанавливают определенные стандарты наблюдаемых величин. Можно осуществлять нормировку приблизительно в следующем порядке сложности:
1) процентные отношения; 2) пропорции; 3) степени; 4) индексы; 5) подклас-
сификация; 6) стандартизация.

Определение первых четырех терминов не должно вызывать сложности
у студентов. Что же касается пятого и шестого, то следует запомнить, что подклассификация подразумевает разделение факторов на «внешние» и «внутренние» (причем внешние факторы не должны изменяться в ходе исследования). Стандартизация же кажется полностью формализованной процедурой. Любой вид арифметического среднего может быть стандартизован при наличии необходимых данных.

В целом, для выработки практических навыков по данной теме, усвоения формул и доведения до автоматизма вычислительных процедур студентам предлагается ряд таблиц, с которыми осуществлялась работа на предыдущем практическом занятии (по нахождению характеристик положения). Необходимо для этих же таблиц определить характеристики рассеяния. На основе совокупных результатов сделать соответствующие выводы. Так же как и на предыдущем занятии, все вычислительные процедуры осуществляются в «ЕХСЕL»,
с учетом всех преимуществ работы с данной программой.

Вопросы и задачи для самоконтроля

1. Определите следующие понятия: варьируемость, вариация, полный диапазон (размах вариации), промежуточный диапазон, интерквартильный диапазон, 10-90% диапазон, дисперсия, рассеяние, среднее квадратическое отклонение, коэффициент вариации.

2. Объясните, почему среднее квадратическое отклонение, а не вариация, обычно используется как мера дисперсии.

3. Можно ли вычислить 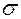качественных данных?

4. Если средний возраст студентов вуза равен 20 годам, а среднее квадратическое отклонение равно 2, то каким будет среднее и сигма (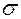) этой группы двадцать лет спустя? Чему будет равен ?

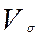5. Население конкретного города состоит из 50% мужчин и 50% женщин; 70% - украинцев - 30% россиян. Можно ли представить переменные одним 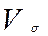? Поясните.

6. Население конкретного города распределено по четырем этническим группам следующим образом: украинцы - 60%, россияне - 20%, татары - 15%, румыны - 5%. Итого: 100%. Вычислите .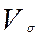

Тема 5. Проверка процедуры первичного измерения на надежность
с использованием математических методов

План

1. Основные показатели надежности измерения в социологической практике. Математические процедуры проверки шкал на надежность.

2. Правильность измерения, выявление систематических ошибок.

3. Устойчивость измерения: показатель абсолютной устойчивости W, средняя квадратическая ошибка, относительные показатели ошибок.

4. Обоснованность измерения как завершающий этап подтверждения надежности измерения.

Методические указания по изучению темы

«Проверка процедуры первичного измерения на надежность
с использованием математических методов»

Центральным понятием данной темы является понятие «надежность». Следует обратить внимание на факт отсутствия единообразия в толковании данного термина применительно к социологической информации. Одни ав­торы трактуют надежность слишком широко, подразумевая качество всего исследования, его итогов. Другие, наоборот, отождествляют надежность лишь с тем или иным ее проявлением (либо с ус­тойчивостью данных, либо с их адекватностью целям исследо­вания и т. п.). К моменту изучения данной темы, основываясь на базисе накопленных социологических знаний (как из предыдущих тем курса «Математические методы в социологии», так и из других дисциплин, ему предшествующих), каждый студент может иметь свою точку зрения относительно изложенного выше. Было бы интересно подискутировать на эту тему
в рамках практического занятия. И все же, необходимо знать, что в строгом смысле слова понятие надежности измерения,как правило, относится именно к инструменту, с помощью которого произво­дится измерение, но не к самим данным, подлежащим измерению. В отношении данных и заключитель­ных выводов исследования используется термин «достоверность».

Из предыдущих курсов студентам уже должно быть известно о том, что
в целом достоверность результатов исследова­ния зависит от многих составляющих, начиная с того, насколько обоснована его общая концепция и все ком­поненты теоретико-методологического раздела програм­мы, от качества исходных данных, системы их сбора (соответствия типа выборки и ее организа­ции целям исследования), качества анализа данных, глубины интерпретации полученных зависи­мостей и связей. Однако следует запомнить, что важной предпосылкой получения достоверных данных, которые бы максимально точно описывали или объясняли существующие социальные реалии, является надежность шкал. В рамках курса «Математические методы в социологии» рассматриваются, соответственно, те операции повышения на­дежности первичного измерения, которые осуществляются посредством математических вычислений. Следует обратить внимание на то, что такие операции используются лишь на стадии отра­ботки инструмента измерения в процессе пилотажа. Итак, в рамках данного курса рассматриваются обобщающие понятия надежности инструмен­та измерения (и, соответственно, надежности данных, фиксируемых этим инструментом), что подразумевает под собой три со­ставляющие: обоснованность, устойчивость и правильность измерения.

Правильность устанавливает общую приемлемость данного метода (способа) измерения и проявляется в выявлении систематических ошибок. Систематические ошибки - это ошибки, которые проявляются постоянно или в соответствии
с определенным законом. К систематическим ошибкам относится: отсутствие разброса ответов по значениям шкалы; использование части шкалы; неравномерное использование отдельных пунктов шкалы; определение грубых ошибок.

В процессе измерения иногда возникают грубые ошибки, причиной которых могут быть неправильные записи исходных данных, плохие расчеты, неквалифицированное использование измерительных средств и т. д., в связи
с чем в рядах измерений могут попадаться данные, резко отличающиеся от совокупности всех остальных значений. Чтобы выяснить, являются ли подобные расхождения результатом грубых ошибок, устанавливается критическая граница таким образом, чтобы вероятность превышения ее крайними значениями была достаточно малой и соответствовала некоторому уровню значимости 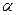. Это правило основано на том, что появление в выборке
чрезмерно больших значений хотя и возможно как следствие естественной
вариабельности значений, но маловероятно.

Например, в случае неравномерного использования отдельных пунктов шкалы для выявления аномалий равномерного распределения по шкале можно предложить следующее правило: для достаточно большой доверительной вероятности (1- 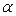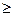0,99) и, следовательно, в достаточно широких границах наполнение каждого значения не должно существенно отличаться от среднего из соседних наполнений. Соответствующий статистический критерий таков: 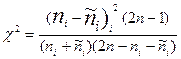. Эта величина имеет Хи-квадрат (далее по тексту - 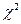) распределение с одной степенью свободы (df = 1). Здесь i - номер значения признака, который подвергается анализу; n_i - наблюдаемая частота для этого значения; 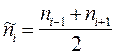- ожидаемая частота, как средняя из двух соседних.

Устойчивость характеризует совпадение результатов измерения при повторных применениях измерительной процедуры и описывается случайными ошибками. Необходимо знать основное правило проведения повторного исследования: оно проводится на одной и той же выборке таким образом, чтобы временной промежуток между исследованиями не был ни слишком коротким (чтобы респонденты не смогли воспроизвести ответы по памяти), ни слишком длинным (чтобы мнение респондентов в отношении предмета исследования не изменилось под влиянием объективных обстоятельств). Как правило, в зависимости от объекта исследования, этот промежуток составляет 2-3 недели.

Результаты обоих исследований заносятся в специальную таблицу. В качестве меры устойчивости шкалы определяют несколько коэффициентов, одним из которых является показатель абсолютной устойчивости шкалы (W). Он рассчитывается по следующей формуле: 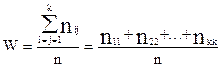, где n_ii - количество совпадающих и в первом и во втором опросе, n - количество опрошенных. W max = 1 - в случае, когда различий между первым и вторым опросом нет, то есть все ответы совпадают. Студентам следует запомнить, что данный коэффициент применяется в основном для качественных признаков номинальной шкалы. Для всех остальных необходимо считать коэффициенты несовпадающих ответов. В этом случае вычисляются показатели неустойчивости, то есть величины ошибки, учитывающие не только факт несовпадения ответов, но
и степень этого несовпадения. Линейной мерой несовпадения оценок является средняя арифметическая ошибка, показывающая средний сдвиг в ответах в расчете на одну пару последовательных наблюдений:

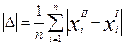, где 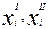- ответы по анализируемому вопросу i -порядка в I
и II пробах соответственно. В качестве показателя для нормирования абсолютной ошибки можно использовать максимально возможную ошибку в рассматриваемой шкале 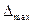. Если число делений шкалы k, тогда 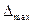равна разнице между крайними значениями шкалы (х_max - х_min), то есть k-1, и относительная ошибка имеет вид: 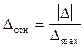, где 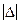- средняя арифметическая ошибка измерения. Важно понять, что для повышения устойчивости шкалы необходимо выяснить различительные возможности ее пунктов. Высокой различимости соответствует малая ошибка.

Обоснованность связана с доказательством того, что был измерен именно тот объект и то свойство, которые требовались, и является самой тяжелой процедурой. Правильность и устойчивость определяются с помощью математических формул, а обоснованность доказывается логическим путем. При доказательстве обоснованности необходимо точно определить предмет и объект, методы и средства измерения.

Проверку надежности необходимо начать с проверки правильности и устойчивости, если они подтверждаются, то, как правило, подтверждается
и обоснованность.

В целом, для закрепления полученных знаний по данной теме и выработки практических навыков на практическом занятии студентам предлагается решить ряд задач, направленных на: 1) нахождение статистических критериев правильности; 2) определение показателей устойчивости.

Вопросы и задачи для самоконтроля

1. Дайте определение надежности измерения. Каковы основные ее составляющие?

2. Что подразумевается под правильностью измерения?

3. Какие типы ошибок могут свидетельствовать о неправильности измерения. Приведите примеры.

4. Назовите основное отличие систематических ошибок от грубых.

5. Дайте определение устойчивости измерения.

6. С разрешением каких ошибок связан вопрос об устойчивости измерения?

7. Измерьте устойчивость проведенного измерения по результатам таблицы, приведенной ниже.

Проба I	Проба II	Сумма

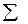8. В чем заключается суть обоснованности измерения и как эта процедура осуществляется?

Модуль ІІ. Измерение связи между признаками с использованием
математических методов

Тема 6. Нормальное распределение как модель вариации.
Критерий линейной взаимосвязи

План

1. Понятие нормального частотного распределения. Характеристики нормальной кривой.

2. Особенности эмпирических распределений.

3. Сравнение эмпирических и теоретических распределений, необходимость и возможности такого сравнения.

4. Критерий линейной взаимосвязи.

Методические указания по изучению темы

«Нормальное распределение как модель вариации.

Критерий линейной взаимосвязи»

В рамках данной темы следует обратить внимание на необходимость сравнения эмпирических распределений с неким эталоном, называющимся идеальным распределением. Студенты должны убедиться в том, что такое сравнение, в исследовательских целях, может быть просто необходимо для: возможности спрогнозировать дальнейшее поведение и развитие того или иного феномена (в случае если различия между эмпирическими и теоретическими распределениями невелики); выявления причин, влияющих на проявление отличий между теоретическими и эмпирическими распределениями (если таковые наблюдаются).

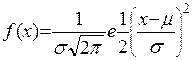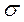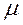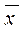Необходимо знать, что к идеальным распределениям можно отнести закон нормального распределения или гауссовский закон распределения. Функция плотности гауссовского распределения имеет вид , где - дисперсия случайной величины, или () - среднее значение (математическое ожидание).

По определению, нормальная кривая состоит из бесконечного числа точек, унимодальна, симметрична и неограничена в обоих направлениях.

Следует запомнить, что различают несколько вариантов эмпирических распределений при сравнении их с теоретическими, а именно: симметрические и скошенные. Студенты должны научиться определять величину скошенности или асимметрии. Для этого вычисляется коэффициент 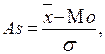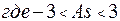. Необходимо запомнить основные свойства асимметрии:
1) коэффициент 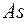изменяется от -3 до +3. Чем ближе 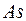к граничным значениям (-3, +3), тем больше скошенность; 2) если значение 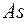положительно, то говорят, что распределение вправо скошено, если отрицательно, то - влево скошено, если 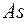=0 - то асимметрии нет, то есть распределение симметрично и .

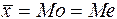Нужно знать, что для оценки различий между теоретическим и эмпирическим распределениями существует критерий Хи-квадрат(далее по тексту – ). Если закон распределения признака неизвестен, но есть основание предположить, что он имеет определенный вид А, то позволяет проверить гипотезу: исследуемая совокупность распределена по закону А (это – Нуль-гипотеза (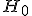), подробно рассматриваемая в рамках следующей темы). Критерий отвечает на вопрос, случайно или нет такое расхождение частот. Важно помнить, что как любой критерий, не доказывает справедливость гипотезы, а лишь
с определенной вероятностью альфа (a) устанавливает ее согласие или несогласие с данными наблюдениями. Если _набл < _табл., то говорят, что распределение приближено к теоретическому с определенной вероятностью альфа (a). Другими словами, 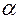– вероятность ошибки утверждения. Чем она меньше – тем лучше, то есть вероятность правильности выбора типа распределения больше,
а различия между наблюдаемыми и теоретическими частотами меньше.

Критерий имеет вид: 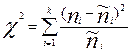. Критическая точка распределения находится по заданному уровню значимости a и числу степеней свободы df. Число степеней свободы находится по формуле: df =(k -1)*(l -1), где k – число строк матрицы, а l – число столбцов матрицы.

Показатель имеет довольно сложное математическое обоснование, однако это очень распространенная величина, полезная в тех статистических ситуациях, когда необходимо измерить расхождение между наблюдаемыми
и ожидаемыми частотами. Последовательность операций в вычислении такова:

1. Вычислить ожидаемые частоты (Е):

,

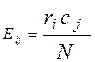где: 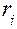– маргинал i -й строки, 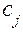– маргинал j- го столбца, а N – объем выборочной совокупности.

2. Вычесть ожидаемые частоты из фактически наблюдаемых частот: (О-Е).

3. Каждую полученную разность возвести в квадрат .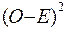

4. Разделить каждое отклонение, возведенное в квадрат, на соответствующую ожидаемую частоту 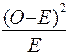(тем самым нормируя каждое абсолютное расхождение на его собственную базу).

5. Сложив все нормированные отклонения, получим . Таким образом, формула будет иметь следующий вид: = .

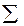
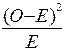Ожидаемая частота в любой клетке вычисляется обычно путем перемножения соответствующих маргиналов и последующего деления их произведения на 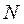. В символах это выглядит так:

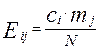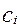, где - маргинал i-й строки, 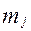- маргинал j-го столбца.

Важно знать, что чисто случайное распределение свидетельствует об отсутствии связи. А вообще, чем больше наблюдаемое распределение приближается к случайному распределению – тем слабее связь между признаками. Подобно этому, чем больше расхождение между наблюдаемым и случайным распределениями, тем сильнее связь или зависимость между переменными. Так как выбран в качестве меры этого расхождения, то чем больше значение , тем теснее взаимосвязь. Таким образом, можно было бы принять как приближенную меру корреляции. Однако значения ненормированы; эти значения не изменяются в пределах от нуля до единицы и, таким образом, непригодны для измерения корреляции в общепринятом смысле слова.

Следует запомнить, что для качественных признаков считается индекс качественной вариации: I = 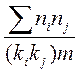100%,

Где: 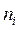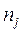_, - частоты качественного признака; 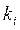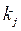_, - теоретические частоты; m - количество градаций.

Этот индекс указывает степень неоднородности полученных ответов, так как для качественных признаков теоретическим является равномерное распределение.

Для альтернативных качественных признаков вариация обычно рассчитывается по следующей формуле: .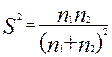

Не менее важным является знание другой меры вариации признака, которая носит название «энтропия», представляет собой меру неопределенности и вычисляется по формуле: .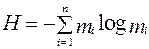

Знак минус в этой формуле отражает тот факт, что вероятности всегда меньше единицы, а логарифм может быть взят по любому основанию.

Из предыдущих тем данного курса студенты должны были усвоить, что среднее квадратическое отклонение показывает, насколько в среднем отличаются все варианты выборки от среднего арифметического. В этой связи необходимо уточнить, что в случае нормального распределения ответы респондентов попадают в отрезок (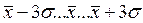). Для качественных признаков, если 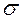близка к нулю, то рассеивания нет. Для центральной вариации справедливо следующее неравенство: Xmin < 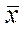, Mo, Me < 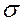< Xmax.

Для количественных признаков чаще всего информационно значимой является 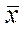(среднее арифметическое), но близка к нему и медиана, которая является вспомогательным коэффициентом и вычисляется в случае, если наблюдается большая скошенность ряда.

В целом,для закрепления знаний по данной теме и выработки практических навыков обработки данных, полученных в ходе социологического исследования, студентам предлагается решить ряд задач, направленных на вычисление и интерпретацию полученных значений. Содержание задач имеет социологический характер, а результаты их разрешения могут рассматриваться
в качестве примера подтверждения первичных и/или постановки вторичных гипотез социологического исследования. Вычислительные процедуры осуществляются в «ЕХСЕL», с учетом всех преимуществ работы в данной программе.

Вопросы и задания для самоконтроля

1. Определите следующие понятия: нормальное распределение, нормальная площадь, нормальная ордината, нормальное отклонение, колоколообразное распределение.

2. Объясните, в каком смысле нормальная кривая является «нормальной».

3. Объясните сущность энтропии.

4. Каким образом распределения делятся по их симметрии? О чем свидетельствуют отклонения от идеальных распределений?

5. Между какими двумя сигма-точками на основной линии нормальной кривой лежат средние 50% случаев?

6. Объясните, почему доля случаев между 0 и 1,0 сигма не равна доле между 1,0 и 2,0?

7. Опишите правила вычисления Хи-квадрат () и его сущность.

Тема 7. Статистическая гипотеза. Проверка статистических гипотез
при анализе социологических данных

План

1. Понятие статистической гипотезы. Проверка статистических гипотез
и сравнимые оценки.

2. Принцип проверки Нуль-гипотезы (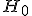). Хи-квадрат () как тест значимости.

3. Нуль-гипотеза (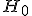): некоторые современные проблемы, связанные
с формулировкой, доказательством/опровержением.

Методические указания по изучению темы

«Статистическая гипотеза. Проверка статистических гипотез
при анализе социологических данных»

В рамках предыдущей темы студенты должны были усвоить, что критерий Хи-квадрат (далее по тексту – ) позволяет сделать вывод относительно закона распределения, которому подчиняется наблюдаемая случайная величина. Однако важно знать, что данный вывод основывается на проверке Нуль-гипотезы (далее по тексту – гипотеза ).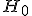

Следует запомнить, что в наиболее распространенном варианте гипотеза 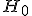утверждает, что данные выборки получены из статистически идентичных совокупностей, а, следовательно, любое различие между выборками является случайной вариацией. Необходимо усвоить, что гипотеза 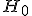выдвигается для того, чтобы потом, как правило, аннулироваться. По своей природе, она тесно связана с более конструктивными статистическими гипотезами, называемыми иногда альтернативными гипотезами. Студенты должны знать, что гипотеза 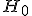идентифицируется с двумя типами исследовательских процедур: 1) сравнением двух или более универсумов в отношении заданного свойства, 2) установлением корреляции между двумя или более свойствами данного универсума. В первом случае она отрицает различие между параметрами совокупностей; во втором – предполагает случайное соотношение или нулевую корреляцию между исследуемыми переменными.

При испытании гипотезы 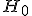наблюдаемое различие рассматривается как отдельное значение в нормальном выборочном распределении, среднее которого равно нулю (что указывает на тождество средних значений генеральных совокупностей), а его квадратическая ошибка при этом оценивается по формуле:

.

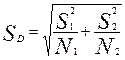В процессе принятия статистического решения необходимо различать два связанных этапа: 1) оценка полученной вероятности;2) оценка последствий неправильного решения.

Отвергая гипотезу 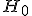, мысленно принимаем некоторую неконкретизированную альтернативную гипотезу, которая имеет свое собственное выборочное распределение. Таким образом, можно сформулировать дилемму: когда риск отклонения правильной гипотезы уменьшается, риск принятия ошибочной гипотезы, соответственно, увеличивается. Какой же вид риска следует предпочесть? Студенты должны понять, что математическая статистика может измерять риск неправильного решения, но она не может посоветовать заинтересованному лицу, принимать или нет этот риск. Принятие измеренного риска будет зависеть от соображений, имеющих субъективный, этический, экономический и т. п. характер. Статистический вывод, тем самым, основывается на весьма нестатистических соображениях.

Следует остановить внимание на основных принципах проверки гипотезы 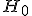: 1) формулируется гипотеза о том, что генеральные совокупности являются однородными; 2) вычисляется комплексный показатель величины наблюдаемых различий, который 3) позволяет определить вероятность получения заданных разностей процентных отношений в предположении гипотезы .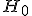

Принятие или отклонение зависит от величины этой вероятности - малая вероятность указывает на ее отклонение, а большая - на принятие.

Студентам важно понять и запомнить, что значение не является мерой степени связи; его уровень значимости указывает лишь на вероятность существования этой связи. Для измерения степени корреляции необходимо обратиться к другим методам (о которых речь пойдет в последующих темах данного курса). Причина этого состоит в том, что, как уже говорилось, выражен
в абсолютных отклонениях и является переменной величиной, а не нормированным показателем, изменяющимся в стандартных пределах от 0 до 1.

Подобно многим другим математическим методам, используемым при статистическом испытании гипотез, методы с использованием применимы лишь тогда, когда выборки сделаны случайно и независимо.

В целом,для закрепления знаний и выработки практических навыков на практическом занятии по теме «Статистическая гипотеза. Проверка статистических гипотез при анализе социологических данных» студентам предлагается ряд задач по вычислению , аналогичных тем, с которыми велась работа на предыдущем практическом занятии. Однако, помимо осуществления вычислительных процедур, студенты должны самостоятельно сформулировать гипотезу для каждого конкретного случая, подтвердить либо опровергнуть ее и сделать соответствующие выводы относительно возможной пользы проделанных операций для изучения того либо иного социального процесса или явления (исходя из содержания конкретной задачи).

Вопросы и задачи для самоконтроля

1. Определите следующие понятия: гипотеза, статистическая гипотеза, нуль-гипотеза, принятие решения, отношение значимости (критическое), выборочное распределение разности, Xи-квадрат (), проверка независимости, проверка однородности.

2. Кандидат заявил, что 60% избирателей должны голосовать за него.
В выборке из 1000 зарегистрированных бюллетеней оказалось 55% голосов, отданных за него. С помощью метода определите правдоподобность заявления кандидата.

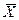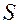3. Заданная выборка имеет следующие характеристики: = 11, = 3, 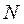=100. Если известно, что истинное среднее значение равно 12, какова ошибка выборки для наблюдаемого среднего? Какова оцениваемая квадратическая ошибка среднего?

4. Может ли случайная выборка, правильно рассчитанная технически, оказаться нерепрезентативной?

Тема 8. Меры взаимосвязи для интервального уровня измерения.
Корреляционный анализ. Уравнение регрессии

План

1. Корреляционное поле как форма графического представления корреляционной зависимости. Виды корреляционного рассеивания.

2. Скедастичность (вариабельность).

3. Корреляционная таблица: техника группирования и основные функции.

4. Общая мера корреляции и ее необходимость.

5. Процедуры измерения линейной корреляции и вычисление наклона линии регрессии.

6. Коэффициент корреляции как мера тесноты, типа и направления связи между двумя признаками.

7. Построение и вычисление уравнения регрессии.

Методические указания по изучению темы «Меры взаимосвязи
для интервального уровня измерения. Корреляционный анализ.

Уравнение регрессии»

В рамках обозначенной темы следует обратить внимание на необходимость и информативность изучения взаимосвязи между признаками в социологическом исследовании. Мерой такой взаимосвязи является коэффициент корреляции. Студенты должны понять смысл термина «correlation» (корреляция). Данный термин состоит из приставки «co-», обозначающей совместность происходящего (по аналогии с «координация») и корня «relation», переводимого как «отношение» или «связь». Дословно correlation – взаимосвязь.

В эмпирической социологии измерение взаимосвязей осуществляется
с использованием математических методов. Однако важно знать, что способы измерения связи могут различаться в зависимости от того, будут данные представлены в форме качественных признаков, которые просто перечислены, или
в виде количественных измерений, и будет ли вид зависимости между переменными простым или сложным.

Студентам необходимо иметь в виду, что формулы измерения связи могут быть удобно сгруппированы на основе двух принципов связи: совместного появления и ковариации. Измерение ковариации (влияния) можно произвести предварительно с помощью корреляционного поля, которое относится к двумерной совокупности данных точно так же, как гистограмма к одномерной совокупности. Любая линия концентрации данных называется линией регрессии.

Следует помнить, что вычисление коэффициентов корреляции возможно с использованием стандартных программ. Итогом данной процедуры будет число, показывающее меру взаимообусловленности в распределении частот появления соответствующих признаков. Студентам необходимо знать, что анализ коэффициентов связи позволяет: 1) выделить факторы, уровень влияния которых слишком низок, что дает возможность исключить их из дальнейшего анализа (гипотеза о наличии связи отрицается); 2) проранжировать оставшиеся связи по уровню взаимной сопряженности (при этом следует иметь в виду, что уровень взаимной сопряженности может определяться как влиянием данного фактора на процесс, так и взаимным изменением данного фактора и процесса под влиянием третьего фактора).

Важно помнить, что тенденция рассеяния не всегда бывает линейной, чаще всего она бывает криволинейной и принимает форму одного из многочисленных видов кривых. Рассеяние значений 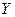, соответствующих данному значению 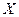, называется скедастичностью. Если степень вариации значений (ширина зоны рассеяния) одинакова для всех значений 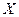, то можно говорить
о том, что переменная 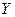гомоскедастична по отношению к X. Гетероскедастичность означает, что степень корреляции неодинакова для всей совокупности.

Связь между признаками изучает корреляционный анализ, а закономерность изменения - регрессионный анализ. Корреляционная зависимость - взаимосвязь между признаками, состоящая в том, что с изменением величины одного признака меняется величина другого. Как правило, при изучении взаимозависимости двух признаков различают: независимые признаки (факторные), которые, чаще всего, обозначаются - 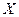и зависимые признаки (результирующие) - 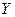. В ходе корреляционного анализа необходимо узнать, как под влиянием факторных признаков изменяется результирующий (если он изменяется вообще) и по какому закону. Корреляционный анализ фиксирует форму, направление и тесноту связи. По типу корреляционная связь может быть прямой или обратной, по форме - прямолинейной или криволинейной, по тесноте - тесной или слабой. Корреляция может быть также парной или множественной. Парная связь устанавливается между двумя признаками (факторным и результирующим). Множественная связь - между большим количеством факторных признаков и результирующим. Корреляционный анализ применяется для объектов, измеренных по интервальной или порядковой шкале, для количественных признаков. Студентам важно знать, что все характеристики корреляционного анализа определяются тремя коэффициентами: коэффициент корреляции - 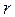; коэффициент регрессии 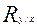; корреляционное отношение 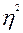(данный коэффициент будет подробно рассматриваться в рамках следующей темы).

Необходимо запомнить, что коэффициент корреляции - это мера тесноты и направления между двумя признаками при линейной связи, обладающая определенными свойствами:

1) = ;

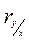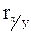2) чем ближе 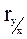к 1 или -1, тем теснее связь. Чем ближе 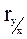к 0, тем связь слабее. Если 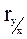= 0, то говорят, что связи нет. Для социальных процессов 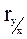редко превышает |0,75|;

3) если 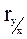> 0, то связь прямая. Если 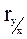< 0, то связь обратная.

Формула вычисления 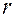может быть представлена в следующем виде:

.

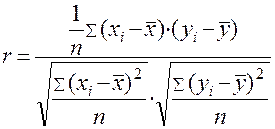Следует иметь в виду, что для сгруппированных данных формула выглядит несколько иначе, а именно:

.

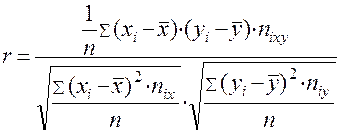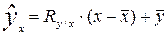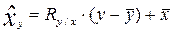Статистическая зависимость одного или большего числа признаков от остальных выражается с помощью уравнений регрессии. Уравнение регрессии описывает числовое соотношение между величинами, выраженное в виде тенденции к возрастанию (или убыванию) одной переменной величины при возрастании (убывании) другой. Для линейной регрессии уравнение имеет вид: или , где 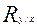, 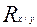- коэффициенты регрессии, которые показывают, насколько в среднем изменится результирующий признак, если факторный изменить на единицу.

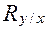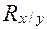Коэффициенты и вычисляются по следующим формулам:

, .

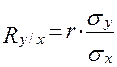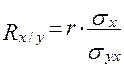Следует запомнить основные свойства коэффициента регрессии:

1) коэффициент регрессии принимает любые значения;

2) коэффициент регрессии не симметричен, т.е. изменяется, есл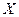и и 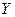поменять местами;

3) единицей измерения коэффициента регрессии является отношение единицы измерения 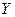к единице измерения ([ ]/[ ]);

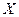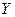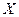4) коэффициент регрессии изменяется при изменении единиц измерения 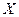и .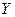

В целом, для закрепления знаний, полученных в рамках изучения данной темы и выработки практических навыков поиска и определения взаимосвязей между признаками, на практическом занятии студентам предлагается решить ряд задач, направленных на вычисление коэффициента корреляции (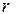) и коэффициента регрессии 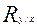. Важно, чтобы студенты не только усвоили соответствующие математические процедуры вычисления, но и умели интерпретировать полученные числовые значения, показывающие факт наличия/отсутствия связи и описывающие ее характер (в случае наличия).

Вопросы и задания для самоконтроля

1. Определите следующие понятия: линия регрессии; линия наименьших квадратов; коэффициент корреляции, коэффициент регрессии.

2. Предположим, что 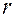= 0,3 для связи между школьными оценками
и часами подготовки. Проанализируйте эту «низкую корреляцию».

3. Для использования 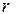требуется, чтобы рассеяние наблюдений относительно линии регрессии было гомоскедастичным. Аргументируйте это утверждение.

4. Возможно ли идеальное прямолинейное рассеяние, если маргинальные распределения являются несхожими? Проиллюстрируйте свой ответ с помощью таблицы или рисунка (графика).

5. Гарантирует ли наличие гомоскедастичности в рассеянии точек линейный вид зависимости? Коротко обоснуйте.

Тема 9. Корреляционное отношение. Нелинейная регрессия.
Множественная и частная корреляция

План

1. Особенности нелинейной регрессии.

2. Вычисление корреляционного отношения. Сравнение статистических показателе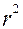й и .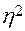

3. Корреляция между двумя и более величинами. Частная и множественная регрессии.

4. Множественная корреляция.