Способом аналитического выравнивания на примере №1

Сущность этого способа заключается в том, что подбирается уравнение, которое наиболее полно отражает характер изменения динамического ряда за изучаемый период. Таким уравнением, в частности, может быть уравнение прямой линии Уt = а + bt, где Уt – выровненное по уравнению значение динамического ряда; t – продолжительность времени; а и b – параметры уравнения, которые необходимо определить. Чтобы определить параметры уравнения, надо решить систему нормальных уравнений: 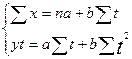, которая отвечает требованию .

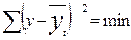Особенности анализа радов динамики заключаются в расчете показателей, которые способствуют выявлению общей тенденции развития явления во времени на основе применения аналитического выравнивания рядов динамики по уравнению прямой линии:

Уt = а + bt(уравнение тренда).

Дня нахождения параметров " а" и " b" составляется табл. 6 исходных и расчетных данных.

Аналитическое выравнивание может быть проведено с использованием различных функций (линейной, показательной, логарифмической, параболы и т.д.). Выбор функции определяется характером изменения ряда динамики.

Параметры уравнения тренда могут рассчитываться упрощенным способом, если t подобрать так, чтобы сумма равнялась нулю, т.е. начало отчета перенести в середину рассматриваемого периода.

При наличии нечетного числа уровней ряда для получения 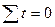средний уровень ряда (t) принимается за ноль. Уровни ряда выше этого уровня (t=0) обозначаются порядковыми числами со знаком минус (-1,-2 и т.д.), а ниже – порядковыми числами со знаком плюс (+1,+2 и т.д.)

При наличии четного числа уровней ряда для получения 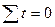уровни ряда от середины обозначаются: - вверх (-1,-3,-5 и т.д.), -вниз (+1,+3,+5 и т.д.).

Таблица 6

Определение тенденции развития явления

Год	Себестоимость 1ц продукции, р.	Время отклонения	Квадрат времени	Произведение себестоимости на время	Выровненный уровень себестоимости 1ц продукции (тренд), р.
n	y	t		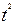у´t	Yt
		-2		-40	19,5+0,3´(-2)=18,9
		-1		-15	19,5+0,3´(-1)=19,2
					19,5+0,3´0=19,5
					19,5+0,3´1=19,8
					19,5+0,3´2=21,1
Итого

Тогда, а= 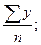b= 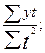в нашем примере 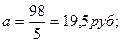b= .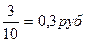

Уравнение тренда: .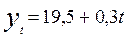

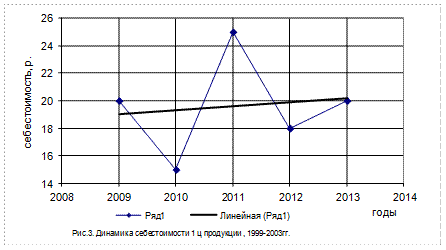
На график заносят как фактические, так и выровненные (расчетные) уровни изучаемого явления по годам, показывающие общую тенденцию развития явления (в нашем примере - изменения себестоимости 1ц продукции) (рис.3).