2015-06-05
6102
Определить с вероятностью 0,954 границы изменения среднего значения признака в генеральной совокупности, если известно следующее ее распределение, основанное на результатах повторного выборочного обследования:
| Группировка значений признака | Число единиц выборочной совокупности, входящих в данный интервал |
| До 4 | |
| 4 – 8 | |
| 8 – 12 | |
| 12 – 16 | |
| 16 – 20 | |
| Итого: 100 |
Решение
Среднее значение признака в генеральной совокупности находится в интервале:
,
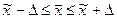где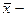 
среднее значение признака в генеральной совокупности, 
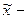среднее значение признака в выборочной совокупности, 
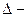предельная ошибка выборочной средней.
Для повторного отбора:
,
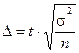где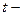 
коэффициент доверия, 
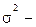дисперсия признака в выборочной совокупности, 
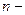объем выборки.
Определяем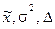 
.
1. Среднее значение признака по выборке:
.
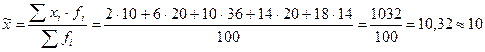2. Выборочная дисперсия:
.
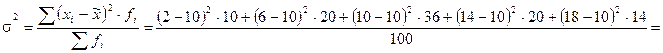
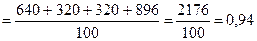Имеем:
, 
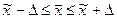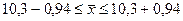и окончательно 
.
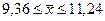Таким образом, с вероятностью 0,954 можно предположить, что среднее значение признака в генеральной совокупности будет находиться в пределах от 9,36 до 11,24.
