ББК 88.36
ISBN 5-9268-0275-7
© А. Д. Наследов, 2004
© М. Г. Филиппова, рисунки., 2004
© Издательство «Речь», 2004
© П. В. Борозсиец, обложка, 2004
КРАТКОЕ СОДЕРЖАНИЕ
Часть I
ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ
Глава 1. Генеральная совокупность и выборка......................................... 19
Глава 2. Измерения и шкалы.....................................................................23
Глава 3. Таблицы и графики....................................................................... 30
Глава 4. Первичные описательные статистики......................................... 40
Глава 5. Нормальный закон распределения и его применение................ 49
Глава 6. Коэффициенты корреляции.......................................................... 64
Часть II
МЕТОДЫ СТАТИСТИЧЕСКОГО ВЫВОДА: ПРОВЕРКА ГИПОТЕЗ
Глава 7. Введение в проблему статистического вывода.......................... 93
Глава 8. Выбор метода статистического вывода.................................... 111
Глава 9. Анализ номинативных данных................................................... 123
Глава 10. Корреляционный анализ........................................................... 147
Глава 11. Параметрические методы сравнения двух выборок............... 162
Глава 12. Непараметрические методы сравнения выборок.................... 172
Глава 13. Дисперсионный анализ (ANOVA)........................................... 185
Часть III МНОГОМЕРНЫЕ МЕТОДЫ И МОДЕЛИ
Глава 14. Назначение и классификация многомерных методов............. 235
Глава 15. Множественный регрессионный анализ.................................. 240
Глава 16. Факторный анализ.................................................................... 251
Глава 17. Дискриминантный анализ......................................................... 282
Глава 18. Многомерное шкалирование................................................... 299
Глава 19. Кластерный анализ................................................................... 329
Приложения. Основные статистические таблицы................................... 353
Англо-русский терминологический словарь........................................... 377
Предметный указатель.............................................................................. 382
Дополнительная литература..................................................................... 389
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ.............................
ПСИХОЛОГИЯ И МАТЕМАТИКА
Часть I
ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ
Глава 1. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ И ВЫБОРКА..................... 1<
Глава 2. ИЗМЕРЕНИЯ И ШКАЛЫ............................................................ Г:
Что такое измерение.............................................................................. 2:
Измерительные шкалы.......................................................................... 24
Как определить, в какой шкале измерено явление.............................. 27
Задачи и упражнения............................................................................. 2S
Глава 3. ТАБЛИЦЫ И ГРАФИКИ............................................................. ЗС
Таблица исходных данных.................................................................... 30
Таблицы и графики распределения частот........................................... 31
Применение таблиц и графиков распределения частот....................... 35
Таблицы сопряженности номинативных признаков............................. 36
Задачи и упражнения............................................................................. 37
Обработка на компьютере..................................................................... 38
Глава 4. ПЕРВИЧНЫЕ ОПИСАТЕЛЬНЫЕ СТАТИСТИКИ...................... 40
Меры центральной тенденции............................................................. 40
Выбор меры центральной тенденции.................................................... 42
Квантили распределения....................................................................... 43
Меры изменчивости............................................................................... 44
Задачи и упражнения............................................................................. 47
Обработка на компьютере..................................................................... 48
Глава 5. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО
ПРИМЕНЕНИЕ.................................................................................... 49
Нормальное распределение как стандарт............................................. 51
ОГЛАВЛЕНИЕ
Разработка тестовых шкал..................................................................... 54
Проверка нормальности распределения............................................... 59
Задачи и упражнения............................................................................. 62
Обработка на компьютере..................................................................... 62
Глава 6. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ............................................ 64
Понятие корреляции.............................................................................. 65
Коэффициент корреляции г-Пирсона.................................................... 67
Корреляция, регрессия и коэффициент детерминации........................ 72
Частная корреляция............................................................................... 75
Ранговые корреляции............................................................................. 77
Коэффициент корреляции /•-Спирмена............................................ 77
Коэффициент корреляции /-Кендалла.............................................. 78
Проблема связанных (одинаковых) рангов...................................... 80
Корреляция бинарных данных.............................................................. 82
Величина корреляции и сила связи....................................................... 84
Какой коэффициент корреляции выбрать............................................. 88
Обработка на компьютере..................................................................... 90
Часть II
МЕТОДЫ СТАТИСТИЧЕСКОГО ВЫВОДА: ПРОВЕРКА ГИПОТЕЗ
Глава 7. ВВЕДЕНИЕ В ПРОБЛЕМУ СТАТИСТИЧЕСКОГО ВЫВОДА.. 93
Гипотезы научные и статистические.................................................... 93
Идея проверки статистической гипотезы............................................. 96
Уровень статистической значимости.................................................... 98
Статистический критерий и число степеней свободы......................... 99
Проверка гипотез с помощью статистических критериев................ 100
Статистическое решение и вероятность ошибки............................... 103
Направленные и ненаправленные альтернативы................................ 106
Содержательная интерпретация статистического решения.............. 108
Глава 8. ВЫБОР МЕТОДА СТАТИСТИЧЕСКОГО ВЫВОДА................ 111
Классификация методов статистического вывода............................. 112
Методы корреляционного анализа...................................................... 114
Методы анализа номинативных данных............................................. 114
Методы сравнения выборок по уровню выраженности признака...... 117
Глава 9. АНАЛИЗ НОМИНАТИВНЫХ ДАННЫХ................................. 123
Анализ классификации: сравнение эмпирического и теоретического
распределений................................................................................. 125
Две градации.................................................................................... 125
Обработка на компьютере: биномиальный критерий.................... 128
Более двух градаций...................................................................... 129
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ПСИХОЛОГИЧЕСКОГО ИССЛЕДОВАНИЯ
Обработка на компьютере: критерий согласия у}.......................... 131
Анализ таблиц сопряженности............................................................ 132
Число градаций больше двух......................................................... 133
Таблицы сопряженности 2x2........................................................... 135
Обработка на компьютере: таблицы сопряженности.................... 141
Анализ последовательности: критерий серий..................................... 142
Обработка на компьютере: анализ последовательности.............. 145
Глава 10. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ.............................................. 147
Корреляция метрических переменных................................................ 148
Частная корреляция.............................................................................. 150
Проверка гипотез о различии корреляций.......................................... 151
Сравнение корреляций для независимых выборок........................ 151
Сравнение корреляций для зависимых выборок............................ 152
Корреляция ранговых переменных..................................................... 153
Анализ корреляционных матриц......................................................... 156
Обработка на компьютере................................................................... 160
Глава 11. ПАРАМЕТРИЧЕСКИЕ МЕТОДЫ СРАВНЕНИЯ ДВУХ
ВЫБОРОК............................................................................................. 162
Сравнение дисперсий........................................................................... 162
Критерий /-Стьюдента для одной выборки......................................... 164
Критерий /-Стьюдента для независимых выборок............................. 165
Критерий /-Стьюдента для зависимых выборок................................. 167
Обработка на компьютере................................................................... 169
Глава 12. НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ СРАВНЕНИЯ
ВЫБОРОК............................................................................................. 172
Общие замечания................................................................................ 172
Сравнение двух независимых выборок............................................... 173
Обработка на компьютере: критерий [/-Манна-Уитни.................. 175
Сравнение двух зависимых выборок................................................... 176
Обработка на компьютере: критерий Г-Вилкоксона..................... 178
Сравнение более двух независимых выборок..................................... 179
Обработка на компьютере: критерий //-Краскала-Уоллеса........... 181
Сравнение более двух зависимых выборок........................................ 182
Обработка на компьютере: критерий %2-Фридмана...................... 184
Глава 13. ДИСПЕРСИОННЫЙ АНАЛИЗ (ANOVA)............................... 185
Назначение и общие понятия ANOVA................................................ 185
Однофакторный ANOVA..................................................................... 189
Обработка на компьютере............................................................... 195
Множественные сравнения в ANOVA................................................. 197
Обработка на компьютере............................................................... 199
ОГЛАВЛЕНИЕ
Многофакторный ANOVA................................................................... 202
Обработка на компьютере............................................................... 212
AN OVA с повторными измерениями................................................. 214
Обработка на компьютере............................................................... 222
Многомерный ANOVA (MANOVA).................................................... 226
Обработка на компьютере............................................................... 228
Часть III МНОГОМЕРНЫЕ МЕТОДЫ И МОДЕЛИ
Глава 14. НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ МНОГОМЕРНЫХ
МЕТОДОВ............................................................................................. 235
Глава 15. МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ.............. 240
Назначение........................................................................................... 240
Математико-статистические идеи метода.......................................... 242
Исходные данные, процедура и результаты....................................... 245
Обработка на компьютере................................................................... 247
Глава 16. ФАКТОРНЫЙ АНАЛИЗ........................................................... 251
Назначение............................................................................................ 251
Математико-статистические идеи и проблемы метода..................... 254
Анализ главных компонент и факторный анализ........................... 254
Проблема числа факторов.............................................................. 259
Проблема общности........................................................................ 260
Методы факторного анализа........................................................... 261
Проблема вращения и интерпретации............................................ 263
Проблема опенки значений факторов............................................ 267
Последовательность факторного анализа...........................,.............. 268
Пример.................................................................................................. 273
Обработка на компьютере................................................................... 277
Глава 17. ДИСКРИМИНАНТНЫЙ АНАЛИЗ.......................................... 282
Назначение........................................................................................... 282
Математико-статистические идеи метода.......................................... 284
Исходные данные и основные результаты......................................... 289
Обработка на компьютере................................................................... 29!
Глава 18. МНОГОМЕРНОЕ ШКАЛИРОВАНИЕ..................................... 299
Назначение........................................................................................... 299
Меры различия..................................................................................... 306
Неметрическая модель........................................................................ 311
Обработка на компьютере............................................................... 314
Модель индивидуальных различий..................................................... 317
Обработка на компьютере............................................................... 321
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ПСИХОЛОГИЧЕСКОГО ИССЛЕДОВАНИЯ
Модель субъективных предпочтений................................................. 324
Обработка на компьютере............................................................... 326
Глава 19. КЛАСТЕРНЫЙ АНАЛИЗ......................................................... 329
Назначение........................................................................................... 329
Методы кластерного анализа.............................................................. 333
Обработка на компьютере: кластерный анализ объектов............. 336
Кластерный и факторный анализ........................................................ 338
Обработка на компьютере: кластерный анализ корреляций......... 340
Кластерный анализ результатов социометрии................................... 342
Обработка на компьютере: кластерный анализ различий............. 346
Кластерный анализ и многомерное шкалирование............................ 347
Приложения ОСНОВНЫЕ СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
Приложение 1. Стандартные нормальные вероятности......................... 353
Приложение 2. Критические значения критерия /-Стыодента............... 355
Приложение 3. Критические значения критерия /-"-Фишера для проверки
направленных альтернатив.................................................................. 357
Приложение 4. Критические значения критерия у}............................... 359
Приложение 5. Критические значения для числа серий......................... 361
Приложение 6. Критические значения коэффициентов корреляции
/•-Пирсона (г-Спирмена)...................................................................... 363
Приложение 7. Значения Z-преобразования Фишера для коэффициентов
корреляции.......................................................................................... 365
Приложение 8. Критические значения критерия /^-Фишера
для проверки ненаправленных альтернатив...................................... 366
Приложение 9. Критические значения критерия (/-Манна-Уитни......... 368
Приложение 10. Критические значения критерия 7-Вилкоксона........... 370
Приложение 11. Критические значения критерия G знаков.................. 371
Приложение 12. Критические значения критерия //-Краскала-Уоллеса 372
Приложение 13. Критические значения критерия х2-Фридмана............ 375
Англо-русский терминологический Словарь.......................................... 377
Предметный указатель............................................................................. 382
Дополнительная литература..................................................................... 389
ПСИХОЛОГИЯ И МАТЕМАТИКА
Более 200 лет назад великий И. Кант со свойственной ему убедительностью обосновывал несостоятельность психологии как науки исходя из того, что психические явления не поддаются измерению, а следовательно, к ним не применимы математические методы. Его соотечественник И. Гербарт противопоставил позиции И. Канта свою точку зрения в книге с названием «Психология как наука, заново обоснованная на опыте, метафизике и математике» (1824-1825). В ней он выражает свое мнение о связи психологии и математики: «Всякая теория, которая желает быть согласованной с опытом, прежде всего должна быть продолжена до тех пор, пока не примет количественных определений, которые являются в опыте или лежат в его основании. Не достигнув этого пункта, она висит в воздухе, подвергаясь всякому ветру сомнений и будучи неспособной вступить в связь с другими уже окрепшими воззрениями»'. Идеи И. Гер-барта к концу XIX столетия воплощаются в жизнь отцами-основателями экспериментальной психологии. С тех пор возможность применения математических методов в психологии перестает вызывать сомнения. Но вопрос о_не-^ обходимости их применения до сих пор вызывает дискуссии. Между тем проблема может быть решена признанием того, что психология — это и наука и искусство. Действительно, искусству практического консультирования или терапии вряд ли необходимо математическое обеспечение. Другое дело область познания, в том числе — того, что лежит в основе различных практических приемов. И здесь уже не достаточно обыденного понимания на уровне здравого смысла, необходим особый инструмент — научный метод, опирающийся на «количественные определения». Почему научное познание не довольствуется здравым смыслом, зачем необходимы математические методы?
Значение математических методов можно понять, сопоставляя обыденное и научное познание. На уровне обыденного познания действительности основным инструментом является здравый смысл. Результат познания — наше мнение (частное, субъективное). Мнение, или точка зрения по поводу той или иной проблемы, необходимо нам для прогноза или интерпретации грядущих реальных событий. Если прогнозы или интерпретации состоятельны, мы укрепляемся в своем мнении, если нет — мы вновь обращаемся к здравому смыслу и корректируем свое мнение, и т. д. Таким образом, продукт обыденного познания — мнение — прежде всего характеризуется как частное, субъек-
 1 Цитируется по кн.: Корнилов К. Н. Учение о реакциях человека с психологической точки прения («Реактология»). М., 1923. С. 3.
1 Цитируется по кн.: Корнилов К. Н. Учение о реакциях человека с психологической точки прения («Реактология»). М., 1923. С. 3.
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ПСИХОЛОГИЧЕСКОГО ИССЛЕДОВАНИЯ
тивное. И все мы хорошо знаем, насколько тяжело бывает переубедить другого человека или отстоять свое мнение. Произведение искусства — это тоже продукт обыденного познания, мнение творца, облеченное в специфическую форму. Эстетические переживания способствуют восприятию и принятию нами авторского мнения. Таким образом, обыденное познание, его продукт — мнение, его инструмент — здравый смысл лежат в основе наших представлений о действительности. А само понятие «обыденное» приобретает смысл в противовес альтернативному — «научному» познанию.
Научное познание по своей конечной цели — совершенству прогнозов и интерпретаций реальных событий — принципиально не отличается от обыденного познания. Более того, научное познание не отменяет и не заменяет обыденного, но добавляет кое-что для совершенствования его результатов — знаний и прогнозов. Наука стремится выйти за пределы частного мнения, сделать знания общезначимыми. В стремлении к общезначимости ученый обосновывает свое мнение эмпирически, при помощи принятых в науке процедур, возводя свое мнение в ранг научной теории. При этом предполагается (и практика это доказывает), что научное познание гарантирует нам более совершенные предсказания и интерпретации действительности.
Научное познание добавляет к инструменту обыденного познания — здравому смыслу — ряд дополнительных процедур, обеспечивая не только убедительность, но и объективность получаемых знаний. Рассмотрим их подробнее. Первый шаг любого (научного) исследования — выражение сомнения в истинности мнения, формулировка мнения как гипотезы — утверждения, допускающего проверку на фактах. Например, я могу поставить под сомнение свою точку зрения о том, что женщины более искусны в общении, чем мужчины. Но чтобы сделать гипотезу доступной проверке при помощи эмпирики, необходимо представить ее в форме математической модели, согласованной со способом регистрации наблюдений. Таким образом, гипотеза содержит указание на математическую модель, форма которой уточняется в соответствии с тем, как будет измерено то, что нас интересует. Моя содержательная гипотеза о большей искусности женщин в общении может быть представлена в форме математической модели: М„ <МЖ (мужчины в среднем менее искусны в общении, чем женщины) или/м </ж (среди мужчин искусные в общении встречаются реже, чем среди женщин). В первом случае предполагается, что я могу вычислить среднюю «искусность в общении» для женщин и для мужчин по результатам ее количественного измерения при помощи некоторой специальной шкалы. Во втором случае достаточно определить частоту встречаемости «искусных в общении» среди мужчин и женщин.
Итак, научное познание начинается с нуждающегося в эмпирической проверке утверждения — гипотезы. Проверка гипотезы предполагает измерение интересующего исследователя явления и обобщение результатов измерения в виде, позволяющем сделать вывод в отношении гипотезы. Измерение и описание предполагает применение различных, хоть и взаимосвязанных, математических моделей и соответствующих им процедур. В процессе измерения мы предстаь-.яем реальные события, явления, свойства в виде чисел, в соответствии
МЕТОДОЛОГИЧЕСКОЕ ВСТУПЛЕНИЕ
с принятой математической моделью измерения. Например, приписываем испытуемому число, обозначающее его пол (1 — мужской, 2 — женский), или ранг, соответствующий успешности выполнения задания (1 — лучше всех, 2 — второе место, и т. д.). Затем множество подобных результатов измерения мы должны представить в виде, доступном интерпретации с точки зрения выдвинутой гипотезы. Для этого используются математические модели описания для обобщения результатов измерения: менее сложные (частоты, средние значения и др.) или более сложные (корреляционный или факторный анализ и др.).
Помимо описания и измерения, существует и третье направление использования математики в психологии — статистическая проверка гипотез. Последнее направление тесно связано с общенаучными канонами экспериментального метода, основанными на статистическом выводе. Отдавая дань истории, отметим, что одним из первых примеров испытания статистической гипотезы была работа Дж. Арбутнота «Довод в пользу божественного провидения, выведенный из постоянной регулярности, наблюдаемой в рождении обоих полов» (1710—1712 гг.)1. Основываясь на том факте, что в течение 82 лет подряд мальчиков каждый год рождалось больше, чем девочек, автор показал, что эти данные опровергают гипотезу о равновероятном рождении мужчин и женщин. Если вероятность рождения мальчика точно равна 0,5, то вероятность того, что на протяжении 82 лет подряд мальчиков будет рождаться больше, чем девочек, равна (У2)82, т. е. она очень мала. По мнению Арбутнота, данный факт — результат вмешательства божественного Провидения, поскольку жизнь муж-чипы находится в большей опасности, чем жизнь женщины.
Общая логика статистической проверки гипотез, или определения статистической достоверности эмпирического результата, сохранилась в общих чертах и до настоящего времени. Возвращаясь к проверке моего мнения о женской искусности в общении, предположим, что я измерил ее при помощи 10-балльной шкалы у 32 женщин и 28 мужчин. Среднее значение для мужчин оказалось равным Л/м = 4,6, а для женщин Мж = 5,1. Здравый смысл мне подсказывает, что факт подтверждает мое мнение. Однако тут же возникает сомнение: достаточно ли столь малого различия в средних значениях, чтобы утверждать, что вообще все женщины в среднем более искусны в общении, чем все мужчины? Какова вероятность, что это все-таки не так? Для ответа на этот вопрос мне и необходимо обратиться к моделям статистического вывода. Если различия статистически значимы, то мое мнение приобретает статус научно обоснованного утверждения.
Таким образом, научное познание, в дополнение к здравому смыслу (но не вместе него!), обязательно предполагает применение математических методов, которые мы представили в виде трех классов моделей: измерения, описания и статистического вывода. Соотношение этих моделей в структуре познания схематично представлено на рис. 1.
Научное познание начинается с формулировки гипотезы — следствия теории или частного мнения по поводу некоторого аспекта реальности. Гипотеза
 Кендалл М., Стьюарт А. Статистические выводы и связи. М., 1973. С. 681.
Кендалл М., Стьюарт А. Статистические выводы и связи. М., 1973. С. 681.
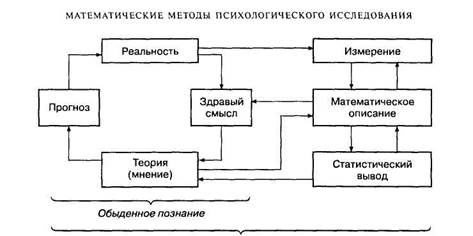
Научное познание Рис. 1. Соотношение обыденного и научного познания
формулируется так, чтобы ее можно было проверить по результатам измерения, то есть в форме описательной математической модели. Описательная математическая модель согласуется с доступной измерительной моделью. Далее модель измерения применяется к интересующим нас аспектам действительности для регистрации результатов наблюдения (как правило — в числовой форме). Результаты измерения обобщаются при помощи описательной математической модели — для представления результатов измерения в доступном для интерпретации виде. Мы обращаемся к здравому смыслу и интерпретируем результаты применения описательных математических моделей. Однако чаще мы этим не ограничиваемся и обосновываем достоверность результатов при помощи соответствующей модели статистического вывода.
Изложенная логика аргументации характерна для науки в целом, в любых ее отраслях, в том числе для психологии. И гуманитарная специфика психологии вовсе не означает принципиального отличия научного метода психологии от методов других наук. Однако такая специфика предмета накладывает свой отпечаток на особенности применения математических методов. Это проявляется, в частности, в применяемых моделях измерения, в том, каким образом мы фиксируем результаты наблюдения непосредственно не видимого и не измеримого (способностей, тревожности и т. д.). Специфика измерительных моделей сказывается на применяемых описательных моделях, а те, в свою очередь — и на моделях статистического вывода.
Иногда можно слышать утверждения, что научный подход с применением математических методов необходим для академических научных исследований, а в практической работе вполне достаточно здравого смысла. Да, практическая деятельность психолога — это прежде всего искусство применения практических методов. Но здравого смысла недостаточно для профессиональной работы. Профессионал отличается тем, что может обосновать свою точку зрения, скажем, проверить эффективность того или иного практического метода или состоятельность организационного решения. При этом он будет опираться на научно обоснованные аргументы, а не только на собственное субъективное мнение.
Глава 1
ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ И ВЫБОРКА
Исследование обычно начинается с некоторого предположения, требующего проверки с привлечением фактов. Это предположение — гипотеза — формулируется в отношении связи явлений или свойств в некоторой совокупности объектов.
ПРИМЕР______________________________________________________________
Исследователь может предположить, что женщины в среднем более тревожны, чем мужчины (тревожность связана с полом). Или что просмотр телепередач, содержащих сцены насилия, повышает агрессивность подростков. В первом случае исследователя интересуют такие явления, как тревожность и пол, а во втором — агрессивность и просмотр телепередач. Объектами-носителями свойств в первом случае будут все мужчины и женщины, а во втором — все подростки.
Для проверки подобных предположений на фактах необходимо измерить соответствующие свойства у их носителей. Но невозможно измерить тревожность у всех женщин и мужчин, как невозможно измерить агрессивность у всех подростков. Поэтому при проведении исследования ограничиваются лишь относительно небольшой группой представителей соответствующих совокупностей людей.
Генеральная совокупность — это все множество объектов, в отношении которого формулируется исследовательская гипотеза.
В первом примере такими генеральными совокупностями являются все мужчины и все женщины. Во втором — все подростки, которые смотрят телепередачи, содержащие сцены насилия. Генеральные совокупности, в отношении которых исследователь собирается сделать выводы по результатам исследования, могут быть по численности и более скромными.
ПРИМЕР______________________________________________________________
При изучении профессионального самоопределения студентов-выпускников некоторого факультета в конкретном вузе генеральная совокупность, казалось бы, весьма невелика и допускает сплошное исследование. Но исследователь обычно
ЧАСТЬ ]. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ
надеется, что выводы исследования будут справедливы не только в отношении выпускников этого, но и последующих годов.
Таким образом, генеральная совокупность — это хотя и не бесконечное пс численности, но, как правило, недоступное для сплошного исследования множество потенциальных испытуемых.
Выборка — это ограниченная по численности группа объектов (в психологии — испытуемых, респондентов), специально отбираемая из генеральной совокупности для изучения ее свойств. Соответственно, изучение на выборке свойств генеральной совокупности называется выборочным исследованием. Практически все психологические исследования являются выборочными, а их выводы распространяются на генеральные совокупности.
Таким образом, после того, как сформулирована гипотеза и определены соответствующие генеральные совокупности, перед исследователем возникает проблема организации выборки. Выборка должна быть такой, чтобы была обоснована генерализация выводов выборочного исследования — обобщение, распространение их на генеральную совокупность. Основные критерии обоснованности выводов исследования — это репрезентативность выборки и статистическая достоверность (эмпирических) результатов.
Репрезентативность выборки — иными словами, ее представительность — это способность выборки представлять изучаемые явления достаточно полно—с точки зрения их изменчивости в генеральной совокупности.
Конечно, полное представление об изучаемом явлении, во всем его диапазоне и нюансах изменчивости, может дать только генеральная совокупность. Поэтому репрезентативность всегда ограничена в той мере, в какой ограничена выборка. И именно репрезентативность выборки является основным критерием при определении границ генерализации выводов исследования. Тем не менее, существуют приемы, позволяющие получить достаточную для исследователя репрезентативность выборки.
Первый и основной прием — это простой случайный (рандомизированный) отбор. Он предполагает обеспечение таких условий, чтобы каждый член гене-
ГЛАВА I. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ И ВЫБОРКА
ральной совокупности имел равные с другими шансы попасть в выборку. Случайный отбор обеспечивает возможность попадания в выборку самых разных представителей генеральной совокупности. При этом принимаются специальные меры, исключающие появление какой-либо закономерности при отборе. И это позволяет надеяться на то, что в конечном итоге в выборке изучаемое свойство будет представлено если и не во всем, то в максимально возможном его многообразии.
ПРИМЕР______________________________________________________________
Изучая агрессивность подростков, исследователь может случайным образом остановить свой выбор на 3 классах разных школ и затем случайным образом отобрать по 10 учащихся из каждого класса. Если же исследователь просит испытуемого пригласить на обследование своих друзей, он грубо нарушает принцип случайности отбора.
Второй способ обеспечения репрезентативности — это стратифицированный случайный отбор, или отбор по свойствам генеральной совокупности. Он предполагает предварительное определение тех качеств, которые могут влиять на изменчивость изучаемого свойства (это может быть пол, уровень дохода или образования и т. д.). Затем определяется процентное соотношение численности различающихся по этих качествам групп (страт) в генеральной совокупности и обеспечивается идентичное процентное соотношение соответствующих групп в выборке. Далее в каждую подгруппу выборки испытуемые подбираются по принципу простого случайного отбора.
ПРИМЕР______________________________________________________________
Исследователь резонно может предположить, что мальчики и девочки различаются как по агрессивности, так и по восприимчивости демонстрируемых по телевидению сцен насилия. Если исследователь планирует обобщить результат исследования влияния телевидения на агрессивность всех подростков, то, руководствуясь социально-демографическими данными, он должен обеспечить идентичное генеральной совокупности соотношение мальчиков и девочек в выборке.
Статистическая достоверность, или статистическая значимость, результатов исследования определяется при помощи методов статистического вывода. Эти методы мы будем подробно рассматривать во второй части этой книги. Сейчас лишь отметим, что они предъявляют определенные требования к численности, или объему выборки.
К сожалению, строгих рекомендаций по предварительному определению требуемого объема выборки не существует. Более того, ответ на вопрос о необходимой и достаточной ее численности исследователь обычно получает слишком поздно — только после анализа данных уже обследованной выборки. Тем не менее, можно сформулировать наиболее общие рекомендации:
□ Наибольший объем выборки необходим при разработке диагностической методики — от 200 до 1000-2500 человек.
ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ
□ Если необходимо сравнивать 2 выборки, их общая численность должна
быть не менее 50 человек; численность сравниваемых выборок должна
быть приблизительно одинаковой.
П Если изучается взаимосвязь между какими-либо свойствами, то объем выборки должен быть не меньше 30—35 человек.
□ Чем больше изменчивость изучаемого свойства, тем больше должен быть
объем выборки. Поэтому изменчивость можно уменьшить, увеличивая
однородность выборки, например, по полу, возрасту и т. д. При этом,
естественно, уменьшаются возможности генерализации выводов.
Зависимые и независимые выборки. Обычна ситуация исследования, когда интересующее исследователя свойство изучается на двух или более выборках с целью их дальнейшего сравнения. Эти выборки могут находиться в различных соотношениях — в зависимости от процедуры их организации. Независимые выборки характеризуются тем, что вероятность отбора любого испытуемого одной выборки не зависит от отбора любого из испытуемых другой выборки. Напротив, зависимые выборки характеризуются тем, что каждому испытуемому одной выборки поставлен в соответствие по определенному критерию испытуемый из другой выборки.
ПРИМЕР______________________________________________________________
Наиболее типичный пример зависимых выборок — повторное измерение свойства (свойств) на одной и той же выборке после воздействия (ситуация «до-после»). В этом случае выборки (одна — до, другая — после воздействия) зависимы в максимально возможной степени, так как они включают одних и тех же испытуемых. Могут быть и более слабые варианты зависимости. Например, мужья — одна выборка, их жены — другая выборка (при исследовании, например, их предпочтений). Или дети 5—7 лет — одна выборка, а их братья или сестры-близнецы — другая выборка.
В общем случае зависимые выборки предполагают попарный подбор испытуемых в сравниваемые выборки, а независимые выборки — независимый отбор испытуемых.
Следует отметить, что случаи «частично зависимых» (или «частично независимых») выборок недопустимы: это непредсказуемым образом нарушает их репрезентативность.
В заключение отметим, что можно выделить две парадигмы психологического исследования. Так называемая R-методология предполагает изучение изменчивости некоторого свойства (психологического) под влиянием некоторого воздействия, фактора либо другого свойства. Выборкой является множество испытуемых. Другой подход, Q-методология, предполагает исследование изменчивости субъекта (единичного) под влиянием различных стимулов (условий, ситуаций и т. д.). Ей соответствует ситуация, когда выборкой является множество стимулов.
Глава 2
 2015-10-16
2015-10-16 3406
3406