Лекция 3.
1. Интегралы вида 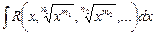 (
(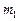 ,
, 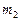 ,…
,… 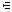
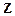 ,
, 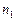 ,
, 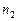 ,…
,… 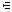
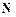 ).
).
2.Интегралы вида 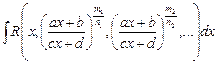 (
(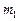 ,
, 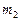 ,…
,… 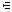
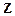 ,
, 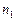 ,
, 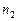 ,…
,… 
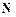 ).
).
3. Интегралы вида 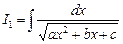 ,
, 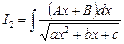 ,
, 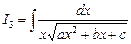 .
.
4. Интеграл от дифференциального бинома 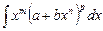 (
( ,
,  ,
, 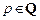 ,
, 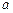 ,
, 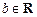 ).
).
1. Интегралы вида 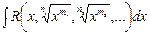 (
(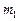 ,
, 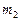 ,…
,… 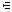
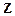 ,
, 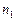 ,
, 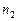 ,…
,… 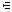
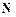 ). Через
). Через 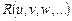 обозначается рациональная функция относительно
обозначается рациональная функция относительно 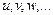 т.е. выражение, которое получено из любых величин
т.е. выражение, которое получено из любых величин 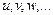 , а также действительных чисел с помощью четырех арифметических действий.
, а также действительных чисел с помощью четырех арифметических действий.
В данных интегралах подынтегральная функция рациональна относительно переменной интегрирования и радикалов от 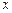 . Они вычисляются подстановкой
. Они вычисляются подстановкой 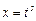 , где
, где 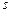 – общий знаменатель дробей
– общий знаменатель дробей 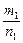 ,
, 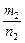 , …. При такой замене переменной все отношения
, …. При такой замене переменной все отношения 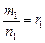 ,
, 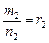 , … являются целыми числами, т.е. интеграл приводится к рациональной функции от переменной
, … являются целыми числами, т.е. интеграл приводится к рациональной функции от переменной 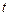 :
:
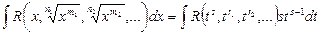 .
.
Пример. Вычислить интеграл 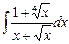 .
.
Решение. Имеем:
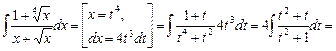
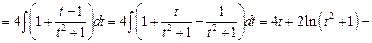
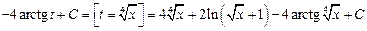 .
.
2. Интегралы вида 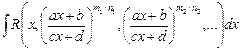 (
( 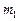 ,
, 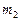 ,…
,… 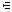
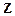 ,
, 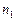 ,
, 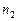 ,…
,… 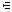
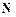 ). Интегралы данного типа подстановкой
). Интегралы данного типа подстановкой
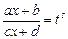 ,
,
где 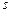 – общий знаменатель дробей
– общий знаменатель дробей 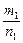 ,
, 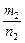 , …, сводятся к интегралам от рациональной функции переменной
, …, сводятся к интегралам от рациональной функции переменной 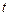 .
.
Пример. Вычислить интеграл 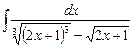 .
.
Решение. Имеем
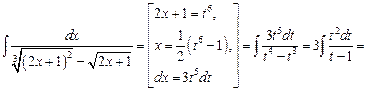
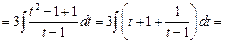
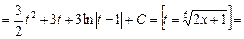
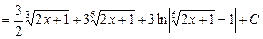 .
.
3. Интегралы вида 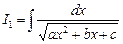 ,
, 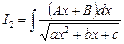 ,
, 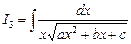 .
.
Для вычисления интеграла 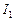 выделяется полный квадрат под знаком радикала:
выделяется полный квадрат под знаком радикала:
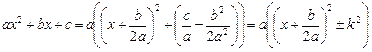
и применяется подстановка 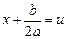 ,
, 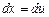 .
.
В результате этот интеграл сводится к табличному:
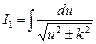 .
.
Для вычисления интеграла 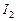 в числителе интеграла выделяется производная выражения, стоящего под знаком радикала, и этот интеграл представляется в виде суммы двух интегралов:
в числителе интеграла выделяется производная выражения, стоящего под знаком радикала, и этот интеграл представляется в виде суммы двух интегралов:
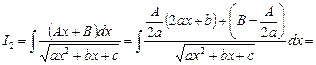
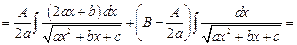
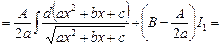
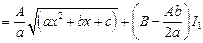 ,
,
где 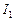 – вычисленный выше интеграл.
– вычисленный выше интеграл.
Вычисление интеграла 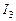 сводится к вычислению интеграла
сводится к вычислению интеграла 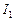 подстановкой:
подстановкой:
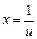 ,
, 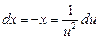 .
.
Пример. Вычислить интеграл 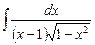 .
.
Решение. Имеем
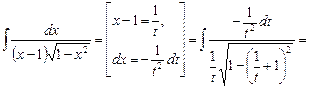
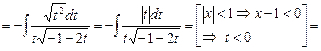
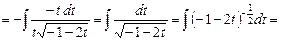
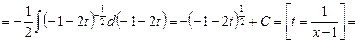
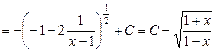 .
.
4. Интегралы вида 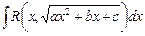 . Частные случаи вычисления интегралов данного вида рассмотрены в предыдущем пункте. Иногда для вычисления данного интеграла используются тригонометрические подстановки.
. Частные случаи вычисления интегралов данного вида рассмотрены в предыдущем пункте. Иногда для вычисления данного интеграла используются тригонометрические подстановки.
Квадратный трехчлен 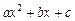 путем выделения полного квадрата и замены переменной можно представить в виде
путем выделения полного квадрата и замены переменной можно представить в виде 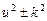 . Таким образом, достаточно ограничиться рассмотрением трех видов интегралов:
. Таким образом, достаточно ограничиться рассмотрением трех видов интегралов:
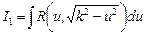 ,
, 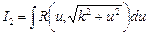 ,
,
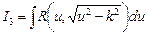 .
.
Интеграл 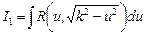 подстановкой
подстановкой 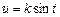 (или
(или 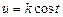 ) сводится к интегралу от рациональной функции относительно
) сводится к интегралу от рациональной функции относительно 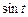 и
и 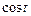 .
.
Интеграл 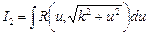 подстановкой
подстановкой 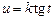 (или
(или 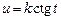 ) сводится к интегралу от рациональной функции относительно
) сводится к интегралу от рациональной функции относительно 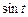 и
и 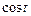 .
.
Интеграл 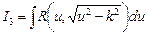 подстановкой
подстановкой 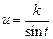 (или
(или 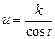 ) сводится к интегралу от рациональной функции относительно
) сводится к интегралу от рациональной функции относительно 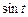 и
и 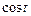 .
.
Пример. Вычислить интеграл 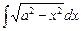 .
.
Решение. Имеем
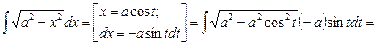
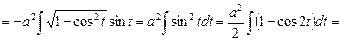
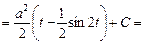
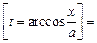
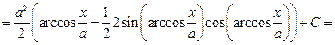
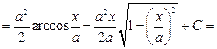
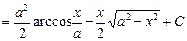 .
.
5. Интегралы вида 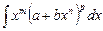 (
(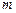 ,
, 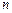 ,
, 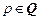 ,
, 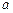 ,
, 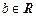 ).
).
Интегралы вида 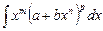 (
(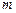 ,
, 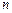 ,
, 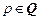 ,
, 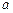 ,
, 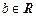 ), называются интегралами от дифференциального бинома
), называются интегралами от дифференциального бинома 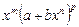 . Эти интегралы выражаются через элементарные функции только в следующих трех случаях:
. Эти интегралы выражаются через элементарные функции только в следующих трех случаях:
1) если 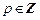 , то используется подстановка
, то используется подстановка 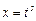 , где
, где 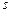 – общий знаменатель дробей
– общий знаменатель дробей 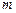 и
и 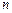 ;
;
2) если 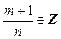 , то используется подстановка
, то используется подстановка 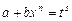 , где
, где 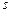 – знаменатель дроби
– знаменатель дроби 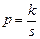 ;
;
3) если 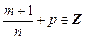 , то используется подстановка
, то используется подстановка 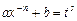 , где
, где 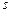 – знаменатель дроби
– знаменатель дроби 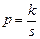 .
.
Во всех остальных случаях, как было показано П.Л. Чебышевым, интегралы от дифференциального бинома не выражаются через элементарные функции.
Пример. Вычислить интеграл 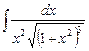 .
.
Решение. Имеем
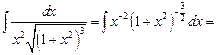
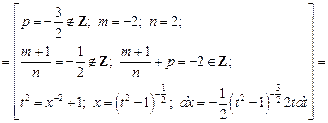
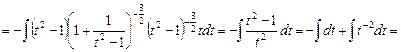
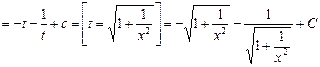 .
.
Вопросы для самоконтроля
1. Как интегрируются интегралы вида 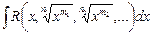 , где
, где 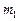 ,
, 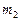 ,…
,… 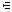
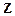 ,
, 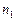 ,
, 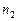 ,…
,… 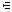
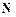 ?
?
2. Какая используется подстановка при интегрировании интегралов вида 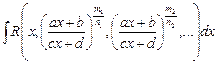 (
(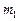 ,
, 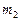 ,…
,… 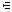
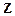 ,
, 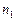 ,
, 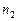 ,…
,… 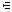
 )?
)?
3. Как интегрируются следующие интегралы 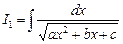 ,
, 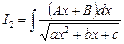 ,
, 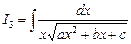 ?
?
4. В каких случаях можно вычислить интеграл от дифференциального бинома 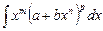 (
(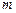 ,
, 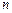 ,
, 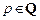 ,
, 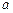 ,
, 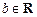 )?
)?
5. Существуют ли интегралы, которые не выражаются через элементарные функции?
 2015-06-05
2015-06-05 890
890








