Теорема 1. Правильную рациональную дробь 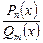 , где
, где 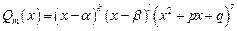 , можно единственным образом разложить на сумму простейших дробей:
, можно единственным образом разложить на сумму простейших дробей:
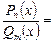
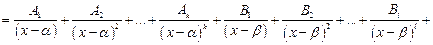
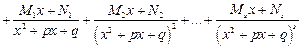 ,
,
где 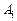 ,
, 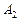 ,
,  ,
, 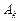 ,
, 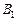 ,
, 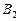 ,
, 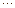 ,
, 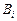 ,
, 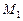 ,
, 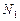 ,
, 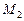 ,
, 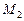 ,
, 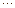 ,
, 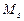 ,
, 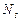 – некоторые действительные числа.
– некоторые действительные числа.
Без доказательства.
Согласно данному разложению, линейным множителям знаменателя 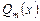 соответствуют простейшие дроби первого и второго типов, а квадратным множителям – третьего и четвертого типов. При этом число простейших дробей, соответствующих данному множителю (линейному или квадратному), равно степени, с которой этот множитель входит в разложение знаменателя дроби. Формула разложения правильной рациональной дроби на простейшие дроби остается справедливой для любого конечного числа линейных и квадратных множителей, входящих в разложение знаменателя
соответствуют простейшие дроби первого и второго типов, а квадратным множителям – третьего и четвертого типов. При этом число простейших дробей, соответствующих данному множителю (линейному или квадратному), равно степени, с которой этот множитель входит в разложение знаменателя дроби. Формула разложения правильной рациональной дроби на простейшие дроби остается справедливой для любого конечного числа линейных и квадратных множителей, входящих в разложение знаменателя 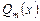 .
.
Пример. Разложить на элементарные дроби 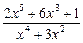
Решение. Выделим из неправильной дроби целую часть, деля числитель на знаменатель
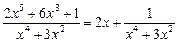 .
.
Разложим полученную в результате дробь на элементарные слагаемые:
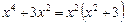 .
.
Тогда 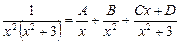 .
.
Для нахождения коэффициентов разложения, чаще всего используется метод неопределенных коэффициентов и метод частных значений.
Метод неопределенных коэффициентов. Суть метода неопределенных коэффициентов состоит в следующем.
- Раскладываем правильную рациональную дробь 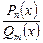 на простейшие дроби с неопределенными коэффициентами.
на простейшие дроби с неопределенными коэффициентами.
- Простейшие дроби приводим к общему знаменателю 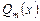 .
.
- Многочлен, получившийся в числителе, приравниваем к многочлену 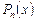 .
.
- Для тождественного равенства двух многочленов необходимо и достаточно, чтобы коэффициенты при одинаковых степенях 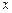 этих многочленов были равны. Учитывая это, приравниваем коэффициенты при одинаковых степенях
этих многочленов были равны. Учитывая это, приравниваем коэффициенты при одинаковых степенях 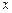 в левой и правой частях полученного тождества. Имеем систему
в левой и правой частях полученного тождества. Имеем систему 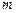 линейных алгебраических уравнений для нахождения
линейных алгебраических уравнений для нахождения 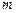 неизвестных коэффициентов
неизвестных коэффициентов 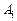 ,
, 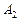 , …,
, …, 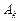 ,
, 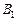 ,
, 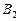 , …,
, …, 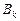 ,
, 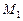 ,
, 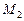 , …,
, …, 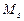 ,
, 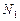 ,
, 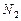 , ….,
, …., 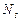 .
.
Пример. Для предыдущего примера, имеем
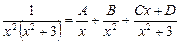 .
.
Приведем к общему знаменателю в правой части
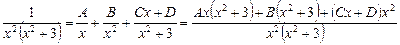 .
.
Отсюда 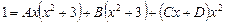
Раскроем скобки в правой части и сгруппируем:
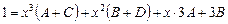 .
.
Приравнивая коэффициенты при одинаковых степенях 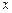 , получаем систему уравнений для нахождения неопределенных коэффициентов
, получаем систему уравнений для нахождения неопределенных коэффициентов 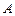 ,
, 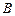 ,
, 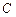 ,
, 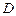 .
.
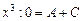 ,
,
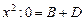 ,
,
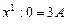 ,
,
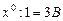 .
.
Отсюда 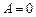 ,
, 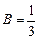 ,
, 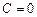 ,
, 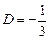 .
.
Следовательно,
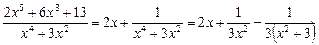 .
.
Метод частных значений.При нахождении неопределенных коэффициентов вместо того, чтобы сравнивать коэффициенты при одинаковых степенях 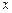 , можно дать переменной
, можно дать переменной 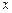 несколько частных значений (по числу неопределенных коэффициентов). Тогда получим систему уравнений относительно неопределенных коэффициентов. Этот метод удобно применять в случае, когда корни знаменателя рациональной дроби
несколько частных значений (по числу неопределенных коэффициентов). Тогда получим систему уравнений относительно неопределенных коэффициентов. Этот метод удобно применять в случае, когда корни знаменателя рациональной дроби 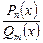 просты и действительны. Тогда последовательно полагают
просты и действительны. Тогда последовательно полагают 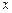 равным каждому из корней знаменателя.
равным каждому из корней знаменателя.
Пример. Разложить рациональную дробь 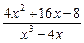 на простейшие.
на простейшие.
Решение. Поскольку 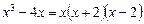 , имеем
, имеем
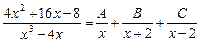 .
.
Приводя правую часть к общему знаменателю, получим:
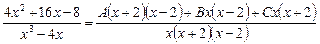 .
.
Отсюда:
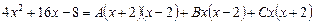 .
.
Придавая 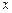 последовательно частные значения, равные корням
последовательно частные значения, равные корням 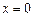 ,
, 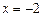 и
и 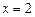 , получим:
, получим:
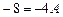 ,
, 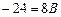 ,
, 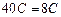 .
.
Отсюда 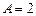 ,
, 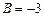 ,
, 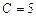 .
.
Таким образом,
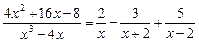 .
.
Иногда для нахождения неопределенных коэффициентов удобно применять комбинацию указанных выше методов, т.е. придавать 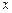 ряд частных значений и приравнивать коэффициенты при некоторых степенях
ряд частных значений и приравнивать коэффициенты при некоторых степенях 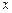 .
.
 2015-06-05
2015-06-05 12352
12352








