Определение 2. Простейшей дробью называется правильная рациональная дробь одного из следующих четырех типов:
1) 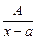 , , | 2) 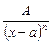 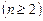 , , |
3) 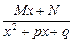 , , | 4) 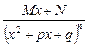 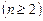 . . |
Здесь 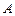 ,
,  ,
, 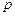 ,
, 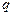 ,
, 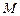 ,
, 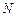 – действительные числа, а квадратный трехчлен не имеет действительных корней, т.е.
– действительные числа, а квадратный трехчлен не имеет действительных корней, т.е. 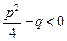 .
.
Простейшие дроби первого типа интегрируются непосредственно с помощью основных правил интегрального исчисления:
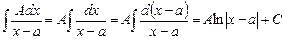 .
.
Дроби второго типа интегрируются непосредственно с помощью основных правил интегрального исчисления:
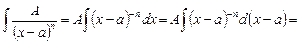
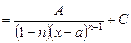 .
.
Интеграл от простейшей дроби третьего типа приводится к табличным интегралам путем выделения в числителе дифференциала знаменателя и приведения знаменателя к сумме квадратов:
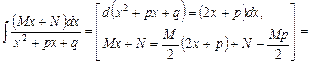
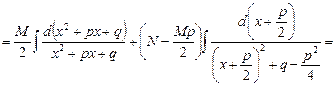
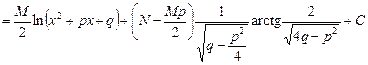 .
.
При интегрировании простейшей рациональной дроби четвертого типа 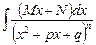 сделаем замену переменной, положив
сделаем замену переменной, положив 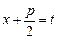 . Откуда
. Откуда 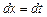 и:
и:
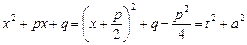 ,
,
где 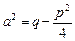 .
.
Тогда
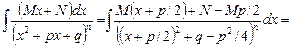
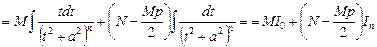 .
.
Вычислим интеграл 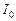 :
:
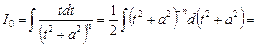
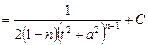 .
.
Для вычисления интеграла 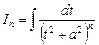 , представим его в виде
, представим его в виде
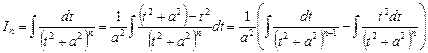
Замечая, что 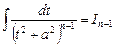 , получаем
, получаем
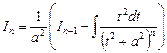 .
.
Вычисление интеграла 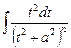 осуществляется с помощью метода интегрирования по частям:
осуществляется с помощью метода интегрирования по частям:
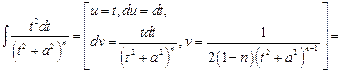
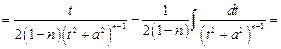
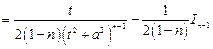
Подставляя найденный интеграл, имеем
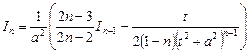 .
.
Данная формула является рекуррентной. Зная табличный интеграл
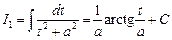 ,
,
находятся интегралы 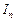 ,
, 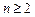 .
.
В частности при 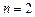 имеем
имеем
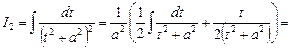
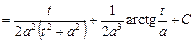 .
.
 2015-06-05
2015-06-05 755
755








