На основе данных таблицы 3 построим следующую модель множественной регрессии, используя пакет «Анализ данных» MS Excel.
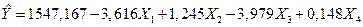 .
.
Из уравнения можно заключить, что:
1) существует обратная зависимость между среднедушевыми доходами населения, прожиточным минимумом и средним размером назначенных пенсий;
2) существует прямая зависимость между среднедушевыми доходами населения, среднемесячной номинальной заработной и ВРП на душу населения.
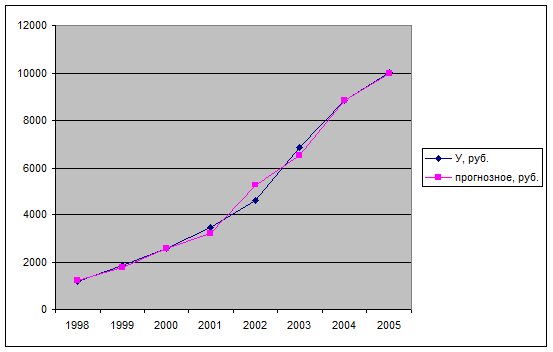
На основе построенной модели можно сравнить прогнозные значения и фактические значения среднедушевых денежных доходов населения (рис.1).
Рисунок 1. Сравнение фактических и прогнозных значений среднедушевых денежных доходов населения (первый вариант)
На основе модели можно также построить следующий график нормальной вероятности (рис. 2).
Рисунок 2. График нормальной вероятности
Говоря о качестве модели, можно отметить, что модель обладает хорошей объясняющей способностью, о чём свидетельствует высокий коэффициент детерминации – 0,992. Так как 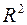 стремится к единице, то уравнение регрессии хорошо аппроксимирует эмпирические данные и использование регрессионной модели теоретически обосновано. Коэффициент детерминации
стремится к единице, то уравнение регрессии хорошо аппроксимирует эмпирические данные и использование регрессионной модели теоретически обосновано. Коэффициент детерминации 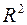 =0,992, что свидетельствует о том, что изменение зависимой переменной
=0,992, что свидетельствует о том, что изменение зависимой переменной 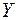 (среднедушевых денежных доходов населения) в основном (на 99,2 %) можно объяснить совместным влиянием включенных в модель объясняющих переменных:
(среднедушевых денежных доходов населения) в основном (на 99,2 %) можно объяснить совместным влиянием включенных в модель объясняющих переменных: 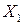 - прожиточный минимум,
- прожиточный минимум, 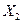 - среднемесячная номинальная заработная плата,
- среднемесячная номинальная заработная плата, 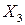 - средний размер назначенных пенсий,
- средний размер назначенных пенсий, 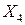 - ВРП на душу населения. Скорректированный коэффициент детерминации
- ВРП на душу населения. Скорректированный коэффициент детерминации 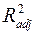 = 0,98. В отличие от
= 0,98. В отличие от 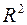 , скорректированный коэффициент детерминации
, скорректированный коэффициент детерминации 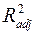 может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенного влияния на зависимую переменную. Следовательно, для оценки адекватности модели множественной регрессии предпочтительнее использовать
может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенного влияния на зависимую переменную. Следовательно, для оценки адекватности модели множественной регрессии предпочтительнее использовать 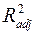 . Этот показатель имеет высокое значение (0,98) и незначительно отличается от
. Этот показатель имеет высокое значение (0,98) и незначительно отличается от 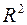 , что говорит о том, что модель обладает хорошей объясняющей способностью.
, что говорит о том, что модель обладает хорошей объясняющей способностью.
Одновременно с этим, проверяя значимость модели по критерию Фишера, можно сказать, что модель статистически значима на уровне значимости 5 %, т.к. 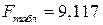 , что существенно меньше полученного фактического значения:
, что существенно меньше полученного фактического значения: 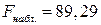 .
.
Говоря о значимости отдельных коэффициентов регрессии, можно сказать, что три из них статистически незначимы, поскольку 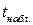 для анализируемой модели составляет 3,18 при уровне значимости 5%. Коэффициент для
для анализируемой модели составляет 3,18 при уровне значимости 5%. Коэффициент для 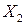 оказывается статистически значимым (Приложение Б).
оказывается статистически значимым (Приложение Б).
Далее проверим модель на наличие мультиколлинеарности с помощью расчёта парных показателей корреляции для каждой пары факторов. Результаты проверки представлены в следующей таблице:
Таблица 4. Таблица парных коэффициентов корреляции
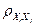
| 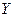
| 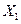
| 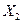
| 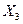
| 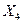
|
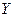
| – | – | – | – | |
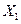
| 0,976 | – | – | – | |
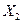
| 0,98 | 0,98 | – | – | |
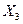
| 0,97 | 0,99 | 0,978 | – | |
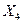
| 0,97 | 0,993 | 0,967 | 0,99 |
Из таблицы видно, что между собой коррелируют все рассматриваемые факторы, в связи с чем необходимо отобрать факторы, которые оказывают наиболее существенное влияние на 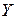 . С этой целью будем постепенно исключать из модели факторы с наибольшим значением парного коэффициента корреляции
. С этой целью будем постепенно исключать из модели факторы с наибольшим значением парного коэффициента корреляции 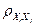 .
.
Из данной таблицы видно, что наибольший парный коэффициент корреляции у переменных 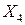 и
и 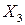 . Исключим из модели фактор
. Исключим из модели фактор 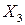 .
.
Получим новую модель:
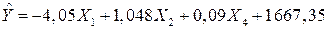 .
.
Рассмотрим таблицу парных показателей корреляции. Из таблицы видно, что между собой коррелируют все оставшиеся факторы. Исключим теперь фактор 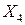 .
.
Полученное уравнение имеет вид:
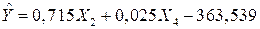 .
.
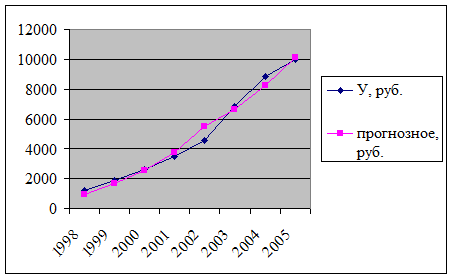 |
На основе построенной модели можно сравнить прогнозные значения и фактические значения показателя среднедушевых доходов населения Санкт-Петербурга.
Рисунок 3. Сравнение фактических и прогнозных значений
среднедушевых денежных доходов населения
Теперь проверим значимость уравнения в целом (адекватность построенной модели линейной регрессии наблюдаемым реальным данным), для этого сформулируем гипотезу 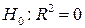 . В данном случае
. В данном случае 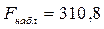 , а
, а 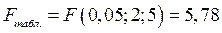 . Так как
. Так как 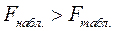 , то нулевая гипотеза отвергается, т.е. линейная модель значима.
, то нулевая гипотеза отвергается, т.е. линейная модель значима.
Проведем тест Дарбина-Уотсона на наличие автокорреляции в остатках. Полученное значение DW=1,68, 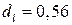 и
и 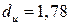 для
для 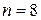 и
и 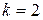 . Следовательно,
. Следовательно, 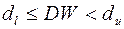 . Это значит, что вывод о наличии автокорреляции не определен.
. Это значит, что вывод о наличии автокорреляции не определен.
Проверим значимость коэффициентов уравнения регрессии. Коэффициент при 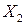 значим, так как
значим, так как 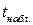 =2,98, что больше
=2,98, что больше 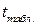 =2,57. Коэффициент при
=2,57. Коэффициент при 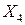 незначим, так как
незначим, так как 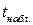 =1,13, что меньше
=1,13, что меньше 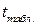 =2,57. Его наличие среди объясняющих переменных не оправдано со статистической точки зрения. Поэтому после установления того факта, что коэффициент незначим, рекомендуется исключить из уравнения регрессии переменную
=2,57. Его наличие среди объясняющих переменных не оправдано со статистической точки зрения. Поэтому после установления того факта, что коэффициент незначим, рекомендуется исключить из уравнения регрессии переменную 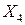 .
.
Рассмотрим парную модель зависимости 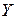 от
от 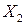 . Корреляционное поле представлено на рис. 4.
. Корреляционное поле представлено на рис. 4.
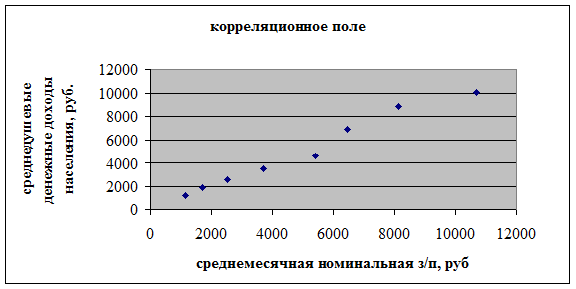
Рисунок 4. Корреляционное поле для 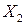
По виду корреляционного поля (рис. 4) можно сделать предположение о линейной зависимости среднедушевых денежных доходов населения от среднемесячной номинальной заработной платы. Проверим гипотезу об их линейной зависимости, для этого оценим тесноту связи. Вычислим средние значения по формулам 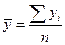 ,
, 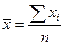 и приведем данные, необходимые для дальнейших вычислений, в следующей таблице (табл.5):
и приведем данные, необходимые для дальнейших вычислений, в следующей таблице (табл.5):
 ;
;

Таблица 5. Расчеты коэффициента корреляции
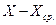
| 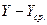
| 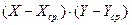
| 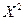
| 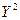
| 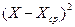
|
| -3824,73 | -3743,35 | 14317284,33 | 1389569,44 | ||
| -3285,33 | -3084,15 | 10132435,1 | |||
| -2461,13 | -2338,65 | 5755709,981 | 6674472,25 | ||
| -1277,33 | -1454,15 | 1857422,149 | |||
| 462,075 | -349,95 | -161703,1463 | 20905012,84 | 213513,3 | |
| 1494,875 | 1929,05 | 2883688,619 | 46938941,44 | ||
| 3183,875 | 3932,95 | 12522021,18 | 78412796,01 | ||
| 5707,675 | 5108,25 | 29156230,82 | 1,14E+08 | 100608924,16 | |
| 76463089,03 | 2,76E+08 | 270334984,1 |
Получим следующие значения для показателей, характеризующих тесноту связи:
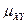 = =
| ||||
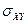 = =
| 3127,966 | 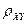 = =
| 0,988037 | |
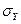 = =
| 3092,622 | 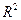 = =
| 0,976216 |
Вывод: так как 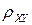 =0,988037, то мы принимаем гипотезу о линейной зависимости между
=0,988037, то мы принимаем гипотезу о линейной зависимости между 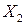 и
и 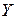 , и связь между ними - весьма высокая. Так как
, и связь между ними - весьма высокая. Так как 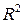 =0,976216, то связь между переменными достаточно сильная и использование линейной регрессионной модели обосновано.
=0,976216, то связь между переменными достаточно сильная и использование линейной регрессионной модели обосновано.
В результате получена модель парной регрессии:
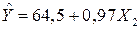 .
.
Проинтерпретируем уравнение регрессии: так как 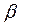 = 0,97, то можно сделать вывод о том, что при увеличении среднемесячной номинальной заработной платы на 1 руб. среднедушевые денежные доходы населения увеличатся на 0,97 руб.
= 0,97, то можно сделать вывод о том, что при увеличении среднемесячной номинальной заработной платы на 1 руб. среднедушевые денежные доходы населения увеличатся на 0,97 руб.
Одновременно с этим, проверяя значимость модели по критерию Фишера, можно сказать, что модель статистически значима на уровне значимости 0,05, так как 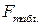 = 5,9, что существенно меньше полученного фактического значения:
= 5,9, что существенно меньше полученного фактического значения: 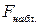 =164.
=164.
Говоря о значимости коэффициентов регрессии, можно сказать, что коэффициент 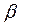 статистически значим, поскольку для анализируемой модели
статистически значим, поскольку для анализируемой модели 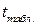 =2,44 при уровне значимости 5 %, а
=2,44 при уровне значимости 5 %, а 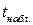 =15,69.
=15,69.
Построим две альтернативные модели: степенную и с квадратным корнем, сравним их с линейной моделью и выберем наилучшую. Для этого прежде всего посчитаем сумму квадратов остатков (ESS) для каждой модели (табл.6-8).
1. Линейная модель.
Таблица 6. Расчет суммы квадратов остатков
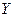 , руб. , руб.
| 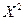 , руб. , руб.
| 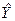
| 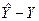
| 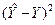
|
| 1178,8 | 1147,9 | 1185,882 | 7,081877 | 50,15297759 |
| 1687,3 | 1712,807 | -125,193 | 15673,24396 | |
| 2583,5 | 2511,5 | 2517,946 | -65,5541 | 4297,340092 |
| 3695,3 | 3674,368 | 206,3682 | 42587,81618 | |
| 4572,2 | 5434,7 | 5373,541 | 801,3411 | 642147,4834 |
| 6851,2 | 6467,5 | 6382,455 | -468,745 | 219721,418 |
| 8855,1 | 8156,5 | 8032,394 | -822,706 | 676845,1879 |
| 10030,4 | 10680,3 | 10497,83 | 467,4261 | 218487,1233 |
| 39377,2 | 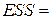
| 1819809,766 |
2. Степенная модель.
Рассмотрим степенную модель вида 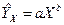 . Линеаризовав данное уравнение, получим систему линейных нормальных уравнений, решив которую получим оценки коэффициентов
. Линеаризовав данное уравнение, получим систему линейных нормальных уравнений, решив которую получим оценки коэффициентов 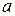 и
и 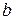 уравнения степенной модели по МНК. В результате имеем значения коэффициентов:
уравнения степенной модели по МНК. В результате имеем значения коэффициентов: 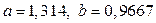 .
.
Следовательно, уравнение регрессии имеет вид:
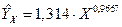 .
.
Найдем сумму квадратов остатков для данной модели:
Таблица 7. Расчет суммы квадратов остатков
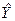
| 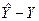
| 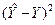
|
| 1192,927 | 14,1267206 | 199,5642 |
| 1731,137 | -106,86348 | 11419,8 |
| 2542,845 | -40,654796 | 1652,812 |
| 3693,614 | 225,613787 | 50901,58 |
| 5362,888 | 790,688217 | 625187,9 |
| 6345,172 | -506,02755 | 256063,9 |
| 7940,636 | -914,46418 | 836244,7 |
| 10304,72 | 274,318647 | 75250,72 |
| ESS= |
3. Модель с квадратным корнем.
Рассмотрим модель вида 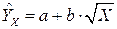 . Используя систему линейных нормальных уравнений, находим оценки параметров модели:
. Используя систему линейных нормальных уравнений, находим оценки параметров модели: 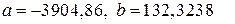 .
.
Следовательно, уравнение регрессии имеет вид:
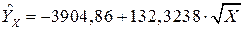 .
.
Найдем сумму квадратов остатков для данной модели:
Таблица 8. Расчет суммы квадратов остатков
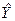
| 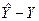
| 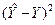
|
| 578,3555 | -600,4445 | 360533,596 |
| 1530,569 | -307,4307 | 94513,6413 |
| 2726,527 | 143,0271 | 20456,7576 |
| 4138,967 | 670,9669 | 450196,569 |
| 5850,105 | 1277,905 | 1633041,09 |
| 6736,721 | -114,4787 | 13105,3652 |
| 8045,745 | -809,3548 | 655055,199 |
| 9770,216 | -260,1844 | 67695,9464 |
| 39377,21 | 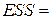
| 3294598,16 |
Вывод: Сумма квадратов остатков равна:
· для линейной модели – 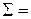 1819809,766;
1819809,766;
· для степенной модели – 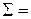 1856921;
1856921;
· для модели с квадратным корнем – 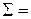 3294598,16.
3294598,16.
Наименьшей из них является сумма квадратов остатков для линейной модели. Следовательно, из рассмотренных моделей она наилучшим образом аппроксимирует исходные статистические данные.
Рассчитаем средний коэффициент эластичности для каждой из трех моделей:
Линейная модель:
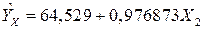 .
.
Средний коэффициент эластичности равен
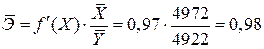 .
.
Степенная модель:
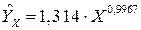 .
.
Средний коэффициент эластичности равен
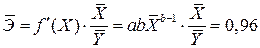 .
.
Модель с квадратным корнем:
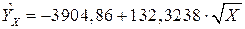 .
.
Средний коэффициент эластичности равен
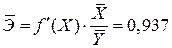 .
.
Вывод. Найдены средние коэффициенты эластичности, наибольшим из них является средний коэффициент эластичности для линейной модели. Следовательно, из рассмотренных моделей она наилучшим образом отражает влияние 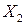 на
на 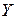 .
.
Оценим с помощью средней ошибки аппроксимации качество уравнений, используя следующую формулу:
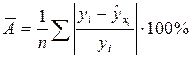 .
.
В таблице 9 приведены расчеты средней ошибки аппроксимации.
Таблица 9. Расчет средней ошибки аппроксимации
| Линейная | Степенная | С квадратным корнем |
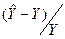
| 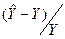
| 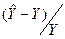
|
| 0,0060077 | 0,011984 | 0,509369 |
| -0,068113616 | 0,058141 | 0,167264 |
| -0,025374144 | 0,015736 | 0,055362 |
| 0,059506389 | 0,065056 | 0,193474 |
| 0,17526378 | 0,172934 | 0,279495 |
| -0,06841787 | 0,07386 | 0,016709 |
| -0,092907592 | 0,10327 | 0,0914 |
| 0,046600939 | 0,027349 | 0,02594 |
| 0,032565586 | 0,528329 | 1,339012 |
Тогда мы получим следующие значения средней ошибки аппроксимации для построенных моделей:
| Линейная модель - A=0,41% |
| Степенная модель -A=6,60% |
| Модель с квадратным корнем - A=16,74% |
Вывод. Средняя ошибка аппроксимации намного меньше для линейной модели. Следовательно, линейная модель наилучшим образом приближает имеющиеся статистические данные. Так как А=0,41%, то данная модель хорошо аппроксимирует данные.
Проведем тест Гольдфельда – Куандта для проверки гипотезы о гомоскедастичности остатков. На основе следующей таблицы (табл.10) составим статистику 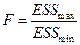 .
.
Таблица 10. Расчеты средней ошибки аппроксимации.
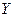 , руб. , руб.
| 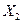 , руб. , руб.
| 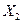
| 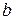
| 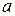
| 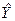
| 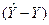
| 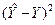
|
| 1178,8 | 1147,9 | 1147,9 | 1,01972 | 49,38858 | 1219,924597 | -41,1246 | 1691,232469 |
| 1687,3 | 1687,3 | 1769,961295 | 68,0387 | 4629,26532 | |||
| 2583,5 | 2511,5 | 2511,5 | 2610,414108 | -26,9141 | 724,3691928 | ||
| 3695,3 | 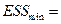
| 7044,86698 | |||||
| 4572,2 | 5434,7 | ||||||
| 6851,2 | 6467,5 | 6467,5 | 0,732079 | 2403,987 | 7138,705868 | -287,506 | 82659,62396 |
| 8855,1 | 8156,5 | 8156,5 | 8375,186885 | 479,9131 | 230316,5979 | ||
| 10030,4 | 10680,3 | 10680,3 | 10222,80725 | -192,407 | 37020,54878 | ||
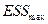 = =
| 349996,7706 |
Вывод: Значение статистика 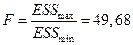 меньше табличного значения
меньше табличного значения 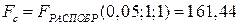 , следовательно, модель гомоскедастична.
, следовательно, модель гомоскедастична.
Далее проведем тест Дарбина-Уотсона на наличие автокорреляции. Рассчитаем статистику DW, используя данные табл.11.:
Таблица 11. Расчеты статистики Дарбина-Уотсона
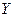 , руб. , руб.
| 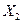 ,руб. ,руб.
| 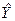
| 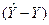
| 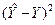
| (e 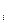 -e -e 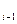 ) )
| (e 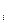 -e -e 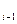 ) ) 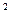
|
| 1178,8 | 1147,9 | 1185,882 | -7,08188 | 50,15297759 | ||
| 1687,3 | 1712,807 | 125,1928 | 15673,24396 | 132,2747 | 17496,59727 | |
| 2583,5 | 2511,5 | 2517,946 | 65,5541 | 4297,340092 | -59,6387 | 3556,77771 |
| 3695,3 | 3674,368 | -206,368 | 42587,81618 | -271,922 | 73941,71407 | |
| 4572,2 | 5434,7 | 5373,541 | -801,341 | 642147,4834 | -594,973 | 353992,7472 |
| 6851,2 | 6467,5 | 6382,455 | 468,7445 | 219721,418 | 1270,086 | 1613117,344 |
| 8855,1 | 8156,5 | 8032,394 | 822,706 | 676845,1879 | 353,9615 | 125288,7456 |
| 10030,4 | 10680,3 | 10497,83 | -467,426 | 218487,1233 | -1290,13 | 1664440,777 |
| 39377,2 | -0,01969 | 1819809,766 | 3851834,703 |
По таблице критических точек распределения Дарбина – Уотсона для заданного уровня значимости 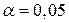 , числа наблюдений
, числа наблюдений 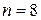 и количества объясняющих переменных
и количества объясняющих переменных 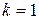 определим два значения:
определим два значения: 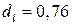 и
и 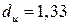 .
.
Так как DW=2,116, то 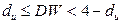 . Это говорит о том, что автокорреляция отсутствует.
. Это говорит о том, что автокорреляция отсутствует.
Среднее значение фактора 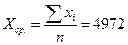 . Прогнозное значение средней заработной платы на этом уровне составит
. Прогнозное значение средней заработной платы на этом уровне составит
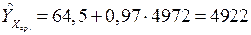 .
.
Увеличение фактора на 5% даст значение 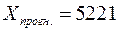 . Тогда
. Тогда
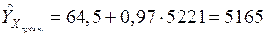 .
.
В процентном отношении: 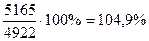 . Итак, увеличение среднего значения фактора на 5% приведет к увеличению значения результата на 243 руб. или на 4,9%.
. Итак, увеличение среднего значения фактора на 5% приведет к увеличению значения результата на 243 руб. или на 4,9%.
Таким образом, можно сделать вывод о том, что модель парной регрессии, которая отражает зависимость между среднемесячной заработной платой и среднедушевыми денежными доходами населения, наилучшим образом подходит для моделирования.
 2015-06-05
2015-06-05 570
570








