Основу для построения модели по общим показателям составляют данные Росстата (табл.12):
Таблица 12. Социальные показатели уровня благосостояния Санкт-Петербурга[7]
| Год | индекс Сена | 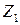 , число родившихся на 1000 населения , число родившихся на 1000 населения
| 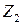 , площадь жилья на 1 чел, кв.м. , площадь жилья на 1 чел, кв.м.
| 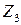 , посещений в смену на 10000 населения , посещений в смену на 10000 населения
| 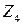 , число преступлений , число преступлений
|
| 2,3 | 7,0 | 18,8 | 321,9 | 101398,0 | |
| 3,9 | 6,6 | 18,9 | 322,1 | 84097,0 | |
| 5,5 | 6,6 | 19,3 | 324,7 | 78680,0 | |
| 4,3 | 6,6 | 19,4 | 327,7 | 89946,0 | |
| 9,0 | 6,2 | 19,8 | 330,4 | 102739,0 | |
| 13,8 | 6,8 | 19,0 | 337,1 | 97704,0 | |
| 19,4 | 7,2 | 20,5 | 341,2 | 90988,0 | |
| 26,0 | 8,1 | 21,0 | 344,7 | 72241,0 | |
| 37,4 | 7,8 | 20,9 | 334,1 | 59849,0 | |
| 46,4 | 8,6 | 21,4 | 336,4 | 71140,0 |
Также при построении модели использовались экономические данные (табл. 13):
Таблица 13. Экономические показатели уровня благосостояния Санкт-Петербурга[8]
| Год | 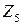 , среднемесячная
номинальная з/п, руб. , среднемесячная
номинальная з/п, руб.
| 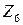 , ВРП на душу населения, руб., до 1998 в тыс.руб. , ВРП на душу населения, руб., до 1998 в тыс.руб.
|
| 212,197 | 9,754 | |
| 781,255 | 13,847 | |
| 1036,938 | 15,898 | |
| 1147,9 | ||
| 1687,3 | 31944,1 | |
| 2511,5 | ||
| 3695,3 | 59212,5 | |
| 5434,7 | 79726,9 | |
| 6467,5 | 95429,3 | |
| 7931,1 | 112506,7 |
Расчет индекса Сена осуществлялся по формуле: 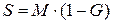 , где
, где 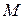 – реальные доходы населения (скорректированные на индекс потребительских цен),
– реальные доходы населения (скорректированные на индекс потребительских цен), 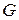 – коэффициент Джини.
– коэффициент Джини.
Для расчета индекса Сена использовались следующие данные (табл. 14):
Таблица 14. Расчет индекса Сена для Санкт-Петербурга в период с 1995 по 2004 год[9]
| год | Среднедушевые доходы, руб. | ИПЦ, % | Коэффициент Джини | 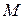
|
| 671,8 | 0,243 | 298,58 | ||
| 923,2 | 125,2 | 0,471 | 737,38 | |
| 1021,8 | 0,395 | 904,25 | ||
| 1178,8 | 0,352 | 662,25 | ||
| 141,1 | 0,309 | 1302,62 | ||
| 2583,5 | 123,5 | 0,341 | 2091,90 | |
| 118,1 | 0,338 | 2936,49 | ||
| 4572,2 | 114,7 | 0,347 | 3986,22 | |
| 6851,2 | 112,2 | 0,388 | 6106,24 | |
| 8855,1 | 112,7 | 0,41 | 7857,23 |
На основе данных таблицы, с использованием пакета «Аналих данных» VS Excel, построим следующую модель множественной регрессии:
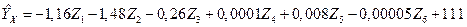 .
.
Из уравнения множественной регрессии получаем, что
· существует обратная зависимость между индексом Сена, числом родившихся, обеспеченностью амбулаторным лечением и площадью жилья на 1 человека;
· существует прямая зависимость между индексом Сена, среднемесячной номинальной заработной и ВРП на душу населения.
На основе построенной модели можно сравнить прогнозные значения и фактические значения индекса Сена (рис. 5).
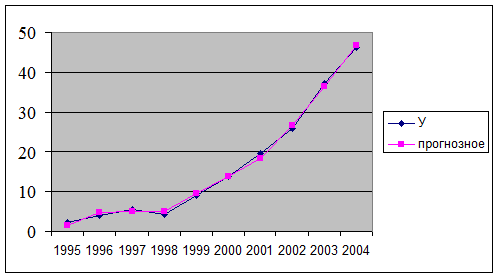
Рисунок 5. Сравнение фактических и прогнозных значений индекса Сена.
Коэффициент детерминации 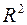 =0,997, что свидетельствует о том, что изменение зависимой переменной
=0,997, что свидетельствует о том, что изменение зависимой переменной 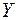 (индекса Сена) в основном (на 99 %) можно объяснить совместным влиянием включенных в модель объясняющих переменных:
(индекса Сена) в основном (на 99 %) можно объяснить совместным влиянием включенных в модель объясняющих переменных: 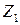 – число родившихся на 1000 населения,
– число родившихся на 1000 населения, 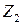 – площадь жилья в среднем на 1 жителя, кв.м,
– площадь жилья в среднем на 1 жителя, кв.м, 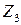 – обеспеченность амбулаторно-поликлиническими учреждениями, посещений в смену на 10000 чел.,
– обеспеченность амбулаторно-поликлиническими учреждениями, посещений в смену на 10000 чел., 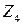 – число зарегистрированных преступлений,
– число зарегистрированных преступлений, 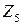 – среднемесячная номинальная заработная плата, руб.,
– среднемесячная номинальная заработная плата, руб., 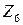 – ВРП на душу населения, руб.
– ВРП на душу населения, руб.
В отличие от 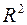 , скорректированный коэффициент детерминации
, скорректированный коэффициент детерминации 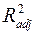 может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенное влияние на зависимую переменную. Следовательно, для оценки адекватности модели множественной регрессии предпочтительнее использовать
может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенное влияние на зависимую переменную. Следовательно, для оценки адекватности модели множественной регрессии предпочтительнее использовать 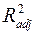 . Этот показатель имеет высокое значение (
. Этот показатель имеет высокое значение (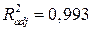 ) и не значительно отличается от
) и не значительно отличается от 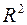 , что говорит о том, что модель обладает хорошей объясняющей способностью.
, что говорит о том, что модель обладает хорошей объясняющей способностью.
Одновременно с этим, проверяя значимость модели по критерию Фишера, можно сказать, что модель статистически значима на уровне значимости 0,05, т.к. 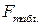 = 8,9, что существенно меньше полученного фактического значения
= 8,9, что существенно меньше полученного фактического значения 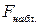 =3381.
=3381.
Говоря о значимости отдельных коэффициентов регрессии, можно сказать, что пять из них статистически незначимы, поскольку 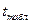 для анализируемой модели составит 3,18 при уровне значимости 5%. Только коэффициент для
для анализируемой модели составит 3,18 при уровне значимости 5%. Только коэффициент для 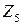 оказывается статистически значимым.
оказывается статистически значимым.
Также некоторые факторы коррелируют друг с другом, в связи, с чем необходимо отобрать факторы, которые будут объясняющими в окончательной модели. С этой целью будем постепенно исключать из модели факторы с наибольшим парным коэффициентом корреляции, полагаясь на логику исследования. В ходе исследования были исключены следующие факторы: 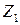 ,
, 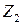 ,
, 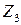 ,
, 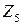 . Получим следующую модель множественной регрессии:
. Получим следующую модель множественной регрессии:
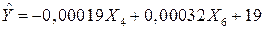 .
.
На основе построенной модели можно сравнить прогнозные значения и фактические значения индекса Сена (рис. 6).
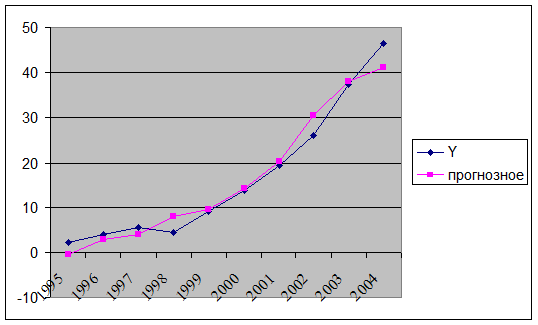
Рисунок 6. Сравнение фактических и прогнозных значений индекса Сена.
Здесь R 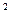 =0,96,
=0,96, 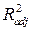 = 0,95. Для оценки адекватности модели множественной регрессии предпочтительнее использовать
= 0,95. Для оценки адекватности модели множественной регрессии предпочтительнее использовать 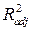 . Этот показатель имеет высокое значение (0,96) и незначительно отличается от
. Этот показатель имеет высокое значение (0,96) и незначительно отличается от 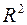 , что говорит о том, что модель обладает хорошей объясняющей способностью.
, что говорит о том, что модель обладает хорошей объясняющей способностью.
Одновременно с этим, проверяя значимость модели по критерию Фишера, можно сказать, что модель статистически значима на уровне значимости 0,05, т.к. 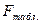 = 4,7, что существенно меньше полученного фактического значения
= 4,7, что существенно меньше полученного фактического значения 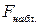 =225.
=225.
Говоря о значимости отдельных коэффициентов регрессии, можно сказать, что они статистически значимы, поскольку 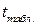 для анализируемой модели составит 1,89 при уровне значимости 10%.
для анализируемой модели составит 1,89 при уровне значимости 10%.
Проведем тест Дарбина-Уотсона на наличие автокорреляции в остатках. Полученное значение DW=1,39; 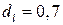 и
и 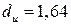 для
для 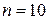 и
и 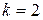 .
.
Следовательно, 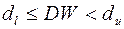 . Что значит, что вывод о наличии автокорреляции не определен.
. Что значит, что вывод о наличии автокорреляции не определен.
Так как 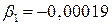 , то можно сделать вывод о том, что при увеличении количества преступлений на единицу, индекс Сена уменьшится на 0,0002. Так как
, то можно сделать вывод о том, что при увеличении количества преступлений на единицу, индекс Сена уменьшится на 0,0002. Так как 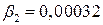 , то можно сделать вывод о том, что при увеличении ВРП на душу населения на 1000 руб. индекс Сена увеличится на 0,32.
, то можно сделать вывод о том, что при увеличении ВРП на душу населения на 1000 руб. индекс Сена увеличится на 0,32.
В целом, можно сказать, что модель множественной регрессии с использованием 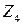 и
и 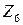 обладает хорошей объясняющей способностью, о чем свидетельствует достаточно высокий нормированный коэффициент детерминации, значимость модели по критерию Фишера и значимость коэффициентов по критерию Стьюдента.
обладает хорошей объясняющей способностью, о чем свидетельствует достаточно высокий нормированный коэффициент детерминации, значимость модели по критерию Фишера и значимость коэффициентов по критерию Стьюдента.
Таким образом, в целом официальные прогнозные оценки об улучшении социально-экономического положения Санкт-Петербурга и увеличении среднедушевых денежных доходов населения совпадают с данными, полученными на основе эконометрического анализа.
 2015-06-05
2015-06-05 538
538








