Затухающие механические колебания. Декремент затухания и добротность системы.
Затухающие колебания - колебания, энергия которых со временем уменьшается. Амплитуда таких колебания является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, часто выражаемых функцией от скорости или её квадрата.
Затухающие колебания пружинного маятника
Пусть имеется система, состоящая из пружины (подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c.
Тогда второй закон Ньютона для рассматриваемой системы запишется так:
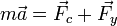
где 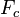 — сила сопротивления,
— сила сопротивления, 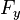 — сила упругости
— сила упругости
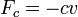 ,
, 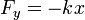 , то есть
, то есть
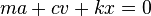
или в дифференциальной форме
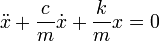
где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления.
Для упрощения вводятся следующие обозначения:
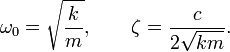
Величину 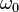 называют собственной частотой системы,
называют собственной частотой системы, 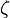 — коэффициентом затухания.
— коэффициентом затухания.
Тогда дифференциальное уравнение принимает вид
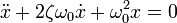
Сделав замену 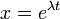 , получают характеристическое уравнение
, получают характеристическое уравнение
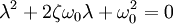
Корни которого вычисляются по следующей формуле
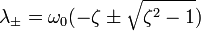
 2015-06-05
2015-06-05 522
522








