Под множеством понимают, следуя основателю теории Г. Кантору, «многое, мыслимое как единое». Другими словами, множество есть совокупность определенных вполне различаемых объектов (субъектов), которые называются элементами, объединенных некоторым свойством. Множества будем обозначать прописными буквами латинского алфавита. В дальнейшем будем считать, что все рассматриваемые нами множества лежат в некотором общем для всех, универсальном множестве, которое обозначим 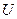 .
.
Множества можно схематично изображать диаграммами (кругами) Эйлера–Венна. Диаграмма Эйлера – Венна состоит из прямоугольника, иллюстрирующего универсальное множество 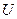 , и замкнутых линий (обычно кругов), все точки внутри которых изображают элементы некоторого множества А. Над множествами можно совершать некоторые операции и задавать между множествами определенные отношения.
, и замкнутых линий (обычно кругов), все точки внутри которых изображают элементы некоторого множества А. Над множествами можно совершать некоторые операции и задавать между множествами определенные отношения.
Два множества А и В равны, если они содержат одни и те же элементы. Обозначение: А=  В. Множество А есть подмножество множества В, если каждый элемент А является элементом и В. Говорят, что А включено в В: А
В. Множество А есть подмножество множества В, если каждый элемент А является элементом и В. Говорят, что А включено в В: А 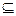 В. Если А
В. Если А 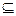 В и
В и 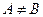 , то множество А есть собственное подмножество множества В:
, то множество А есть собственное подмножество множества В: 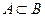 .
.
Вообще для произвольных двух множеств А и В возможны 3 варианта отношений.
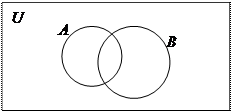
Вариант 1 – множества А и В имеют общие элементы:
 |
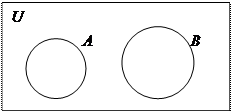
Вариант 2 – множества А и В не имеют общих элементов:
 |
Вариант 3 – одно из множеств является собственным подмножеством другого:
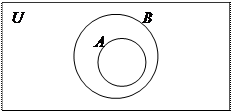 | |||
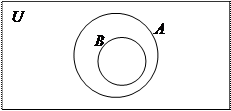 |
или
Дополнениеммножества 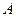 до универсального множества
до универсального множества 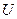 называется множество
называется множество 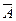 , элементы которого не принадлежат
, элементы которого не принадлежат 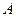 .
.
Пересечениемдвух множеств А и В называется множество A 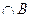 , состоящее изэлементов, принадлежащих одновременно и множеству А, и множеству В.
, состоящее изэлементов, принадлежащих одновременно и множеству А, и множеству В.
Объединением множеств А и В называется множество A 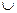 B, состоящее изэлементов, принадлежащих хотя бы одному из множеств А или В.
B, состоящее изэлементов, принадлежащих хотя бы одному из множеств А или В.
Разностьюмежду множествами А и В называется множество 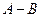 , состоящее изэлементов множества А, которые не принадлежат множеству В.
, состоящее изэлементов множества А, которые не принадлежат множеству В.
Симметрической разностьюмножеств А и В называется множество 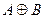 (
(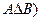 , равное объединению двух разностей
, равное объединению двух разностей 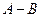 и
и 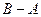 .
.
Порядок выполнения операций в выражениях определяется следующим образом. Прежде всего выполняется операция дополнения множества до универсального множества 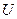 . Затем выполняются последовательно слева направо действия, заданные в скобках. Пересечение считают теоретико-множественным умножением, а объединение – теоретико-множественным
. Затем выполняются последовательно слева направо действия, заданные в скобках. Пересечение считают теоретико-множественным умножением, а объединение – теоретико-множественным
сложением. Поэтому сначала выполняют операцию пересечения и только после нее – объединения или разности. Пересечение и объединение рассматривают как умножение и сложение в силу того, что своими свойствами они напоминают эти арифметические операции. По этой же причине пустое множество 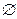 похоже на число 0, а универсальное множество
похоже на число 0, а универсальное множество 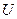 – на число 1.
– на число 1.
Законы теории множеств, верные для любых множеств А, В, С.
1. A Ç B = B Ç A – закон коммутативности пересечения.
2. A È B = B È A – закон коммутативности объединения.
3. A Ç(B Ç C) = (A Ç B)Ç C – закон ассоциативности пересечения.
4. A È(B È C) = (A È B)È C – закон ассоциативности объединения.
5. A Ç(B È C) = (A Ç B)È(A Ç C)– закон дистрибутивности пересечения относительно объединения.
6. A È(B Ç C) = (A È B)Ç(A È C) – закон дистрибутивности объединения относительно пересечения.
7. A Ç A = A – закон идемпотентности пересечения.
8. A È A = A – закон идемпотентности объединения.
9. A ÇÆ = Æ. 10. A ÈÆ= A. 11. A Ç 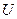 = A. 12. A È
= A. 12. A È 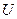 =
= 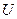 .
.
13. A Ç 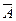 =Æ – закон противоречия. 14. A È
=Æ – закон противоречия. 14. A È 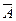 =
= 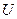 – закон исключенного третьего.
– закон исключенного третьего.
15. 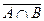 =
= 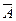 È
È 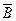 – закон де Моргана для дополнения пересечения.
– закон де Моргана для дополнения пересечения.
16. 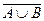 =
= 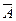
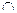
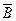 – закон де Моргана для дополнения объединения.
– закон де Моргана для дополнения объединения.
17. A Ç(B È A) = A – закон поглощения. 18. A È(B Ç A) = A – закон поглощения.
19. (A Ç B)È(A Ç 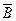 ) = A – закон склеивания. 20. (A È B)Ç(A È
) = A – закон склеивания. 20. (A È B)Ç(A È 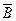 ) = A – закон склеивания.
) = A – закон склеивания.
21. A = 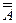 – закон инволюции. 22. A - B = A Ç
– закон инволюции. 22. A - B = A Ç 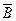 . 23. A Å B = (A È B) -(A Ç B).
. 23. A Å B = (A È B) -(A Ç B).
Замечание 1. Очевидно, что 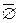 =
= 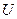 и
и 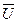 = Æ.
= Æ.
Замечание 2. Законы де Моргана можно распространить на большее число
множеств.
 2015-06-05
2015-06-05 282
282








