2015-06-05
943
Задача 3.1 Задано универсальное множество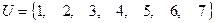 
, множества 
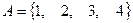и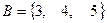 
. Изобразить множества с помощью кругов Эйлера-Венна. Выполнить действия 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
.
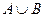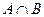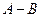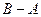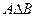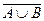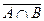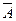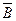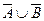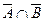Решение. Изобразим данные множества с помощью кругов Эйлера-Венна
 |
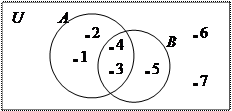Выполним действия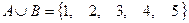 
, 
, 
, 
, =(
, 
, 
, 
, = 
, = 
.
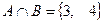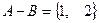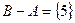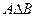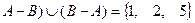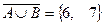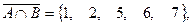
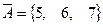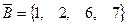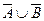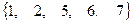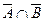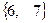Задача 3.2 Задано универсальное множество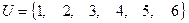 
, множества 
, 
, 
, 
, 
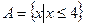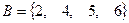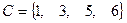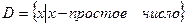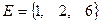. Найти множество 
.
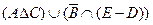Решение. Зададим множества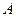 
и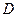 
перечислением элементов 
, 
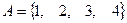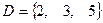. Выполним последовательно действия: 
, 
, 
, 
, 
.
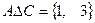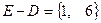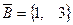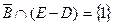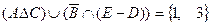Задача 3.3 Доказать справедливость утверждения A Å(B - A Ç B) = A È B с помощью таблицы принадлежности и используя законы теории множеств.
Решение.
Составим таблицу принадлежности, рассмотрев четыре возможных случая принадлежности некоторого элемента двум множествам:
| A | B | A Ç B | B - A Ç B | A Å(B - A Ç B) | A È B |
| - | - | - | - | - | - |
| - | + | - | + | + | + |
| + | - | - | - | + | + |
| + | + | + | - | + | + |
Результаты выполнения действий над множествами в левой и правой частях совпадают, значит, утверждение справедливо.
Применим законы логики.
Возьмем левую часть A Å(B - A Ç B) данного равенства и сведем ее к правой части A È B.
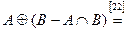
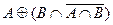
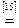
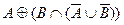
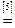
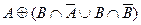
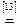
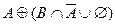
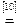
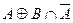
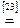
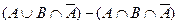
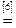
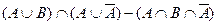
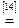
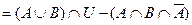
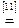
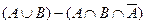
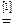
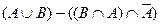
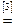
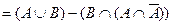
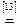
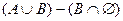
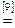
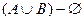
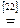
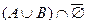
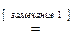
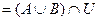
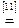
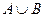. Утверждение справедливо.
