Функция 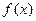 , полином Жегалкина которой имеет вид
, полином Жегалкина которой имеет вид 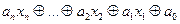 , принадлежит классу линейных функций L:
, принадлежит классу линейных функций L: 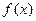
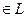 . Если для двух кортежей длины n из нулей и единиц
. Если для двух кортежей длины n из нулей и единиц 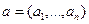 и
и 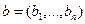 выполнены условия
выполнены условия 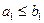 , …,
, …, 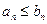 , то говорят, что
, то говорят, что 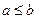 . При невыполнении этих условий кортежи
. При невыполнении этих условий кортежи 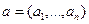 и
и 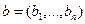 несравнимы. Кортежи разной длины не сравнивают.
несравнимы. Кортежи разной длины не сравнивают.
Функция 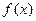 называется монотонной, если для всех корежей
называется монотонной, если для всех корежей 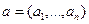 и
и 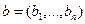 из условия
из условия 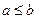 следует, что
следует, что 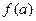
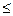
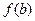 , монотонная функция принадлежит классу монотонных функций M:
, монотонная функция принадлежит классу монотонных функций M: 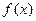
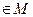 .
.
Функция 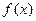 принадлежит классу функций, сохраняющих константу 0, если
принадлежит классу функций, сохраняющих константу 0, если 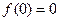 :
: 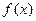
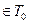 .
.
Функция 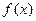 принадлежит классу функций, сохраняющих константу 1 если
принадлежит классу функций, сохраняющих константу 1 если 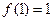 :
: 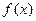
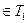 .
.
Функция 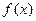 принадлежит классу самодвойственных функций, еслидля всех кортежей выполняется условие
принадлежит классу самодвойственных функций, еслидля всех кортежей выполняется условие 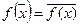 :
: 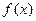
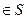 .
.
Система булевых функций называется полной, если любая булева функция является суперпозицией ((композицией) функций этой системы. Теорема Поста: система булевых функций является полной, если она целиком не принадлежит ни одному классу 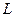 ,
, 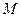 ,
, 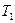 ,
, 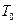 ,
, 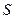 .
.
 2015-06-05
2015-06-05 272
272








