Задача 3.1 Определите полноту системы функций 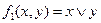 ,
, 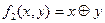 .
.
Решение. Определим принадлежность функций каждому классу 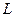 ,
,  ,
, 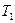 ,
, 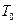 ,
, 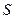 .
.
Построим таблицы истинности
| x | y | 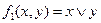
| 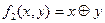
|
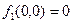 , значит,
, значит, 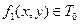 ;
; 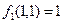 , значит,
, значит, 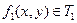 ;
; 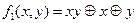 , значит,
, значит, 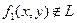 ;
; 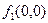
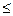
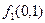
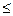
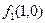
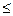
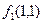 , значит,
, значит, 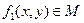 ;
;
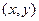
| 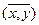
| 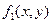
| 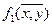
| 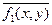
|
| (0,0) | (1,1) | |||
| (0,1) | (1,0) |
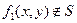 .
.
Аналогично, проводим исследование 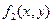 . Результаты удобно занести в таблицу
. Результаты удобно занести в таблицу
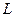
| 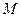
| 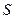
| 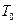
| 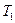
| |
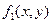
| - | + | - | + | + |
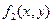
| + | - | - | + | - |
Из таблицы видно, что система целиком не принадлежит одному классу, по теореме Поста эта система функций является полной.
Практическое задание
4.1 Определить полноту системы функций.
Вариант 1
а) 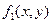 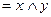 , , 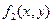 =0, =0, 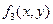 = = 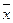 ;
б) ;
б) 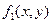 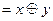 , , 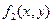 =1, =1, 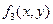 = = 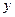
| Вариант 2
а) 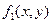 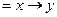 , , 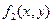 =1, =1, 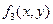 = х;
б) = х;
б) 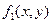 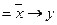 , , 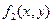 =0, =0, 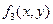 = = 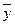
|
Вариант 3
а) 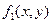 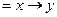 , , 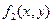 = y, = y, 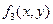 = = 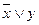 ;
б) ;
б) 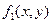 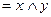 , , 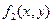 =0, =0, 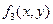 = = 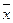
| Вариант 4
а) 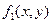 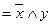 , , 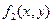 = = 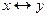 , , 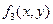 = = 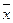 б) б) 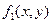 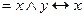 , , 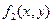 =1, =1, 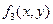 = = 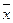 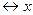
|
Контрольные вопросы
1) Дайте определение полной системы функций.
2) Дайте определение линейной функции.
3) Дайте определение монотонной функции.
4) Дайте определение самодвойственной функции.
5) Дайте определение функции, сохраняющей константу 0.
6) Дайте определение функции, сохраняющей константу 1.
7) Сформулируйте теорему Поста.
 2015-06-05
2015-06-05 248
248







