Задача 3.1 Построить полином Жегалкина для функции, таблица истинности которой имеет следующий вид:
| х | y | z | f(x,y,z) |
Решение.
Применим метод неопределённых коэффициентов. Общий вид полинома Жегалкина для функции от трёх переменных имеет вид 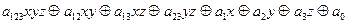 . Будем поочерёдно подставлять кортежи значений аргумента и приравнивать значениям функции: 1) f(0,0,0)=0,
. Будем поочерёдно подставлять кортежи значений аргумента и приравнивать значениям функции: 1) f(0,0,0)=0, 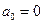 , 2) f(0,0,1)=1,
, 2) f(0,0,1)=1, 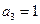 , 3) f(0,1,0)=1,
, 3) f(0,1,0)=1, 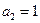 , 4) f(0,1,1)=0,
, 4) f(0,1,1)=0, 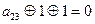 ,
, 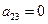 , 5) f(1,0,0)=0,
, 5) f(1,0,0)=0, 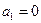 , 6) f(1,0,1)= 1,
, 6) f(1,0,1)= 1, 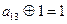 ,
, 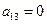 , 7) (1,1,0)=0,
, 7) (1,1,0)=0, 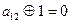 ,
, 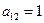 , 8) f(1,1,1)=0,
, 8) f(1,1,1)=0, 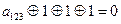 ,
, 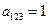 . Полином Жегалкина для функции равен f(x,y,z)=
. Полином Жегалкина для функции равен f(x,y,z)= 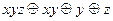 .
.
Практическое задание
4.1 Построить полином Жегалкина.
Вариант 1 а) 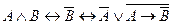 б) б) 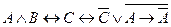 в) в) 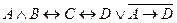 . . | Вариант 2 а) 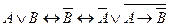 б) б) 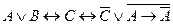 в) в) 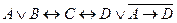 . . |
Вариант 3 а) 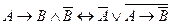 ; б) ; б) 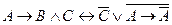 ; в) ; в) 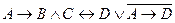 . . | Вариант 4 а) 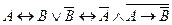 ; б) ; б) 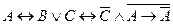 ; в) ; в) 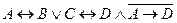 . . |
Контрольные вопросы
1) Дайте определение полинома Жегалкина.
2) Каков алгоритм построения полинома Жегалкина?
Практическая работа № 10.
 2015-06-05
2015-06-05 893
893








