2015-06-10
4707
Исходными данными являются:
- производительность фильтра V, м3/ч;
- плотность твердой фазы ρт, кг/м3;
- массовая концентрация твердой фазы в исходном осадке х, кг/кг;
- форма частиц, размер частиц l, d, мкм;
- скорость осаждения частиц w ос, мм/с;
- плотность фильтрата ρ, кг/м3;
- конечная массовая доля влаги в осадке, %;
- динамический коэффициент вязкости фильтрата µ, Па·с.
При предварительном выборе типа фильтра можно ориентироваться на данные табл. 7.12. Окончательный выбор делается после его проверки в лабораторных или полупромышленных условиях.
Таблица 7.12
Влияние свойств суспензии на выбор типа фильтра
| Свойства суспензий | Тип фильтра | ||
| Скорость осаж- дения твердой фазы, мм/с | Объемная концентрация, % | Скорость образования осадка, мм/мин | Скорость фильтрования, 104 м/с |
| Не ограничены | Емкостные Фильтр-прессы рамные Фильтр-прессы горизонтальные Листовые Патронные Барабанные с наружной фильтрующей поверхностью Барабанные с внутренней фильтрующей поверхностью Ленточные Тарельчатые и карусельные Барабанные с намывным слоем Дисковые | ||
| <18 Не ограничена Медленно Медленно <18 >12 >12 >12 Медленно | Не ограничена >1 >1; <1 – с на- мывным слоем >1; <1 – с на- мывным слоем >5 >20 >10 >10 <5 >5 | <10 >1 Не ограничена Не ограничена >1 >2 >1 >8 <1 >2,7 | <400 >0,08 <1,7 <1,7 400-0,2 >400 >1,7 >1,7 <1,7 >1,7 |
Промышленное фильтрование проводят чаще всего при постоянном перепаде давления.
При Δ р = const объем фильтрата, прошедшего через 1 м2 площади фильтрующей поверхности, V, м3/м2, за время τ, и продолжительность фильтрования τ связаны уравнением
V 2 + 2 KС = K τ, (7.3)
где С – константа фильтрования, характеризующая гидравлическое сопротивление фильтрующей перегородки (ткани), м3/м2; K – константа фильтрования, учитывающая режим процесса фильтрования и физико-химические свойства осадка и жидкости, м2/с; τ – продолжительность фильтрования, с.
Константы фильтрования K и C определяются экспериментально.
Уравнение
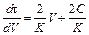, (7.4)
выражающее прямолинейную зависимость между величинами d τ /dV и V, применяется для определения констант C и K по экспериментальным данным. Для этой цели откладывают по оси абсцисс измеренные значения V 1, V 2, …, а по оси ординат – соответствующие измеренные значения Δτ1 /Δ V 1 , Δτ2 /Δ V 2 и т.д. Проведя по экспериментальным точкам прямую (рис. 7.17), находят затем K и С по уравнению
. (7.5)
Скорость фильтрования, м3/(м2 ·с), в данный момент, определенная по зависимости
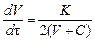, (7.6)
представляет собой удельную производительность фильтра V уд .
Константа фильтрования K, м2/с, отнесенная к 1 м2 фильтрующей поверхности, при Δ р = const связана с удельным сопротивлением осадка уравнением
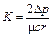, (7.7)
где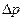 
– перепад давлений на фильтре, Па; μ – динамический коэффицент вязкости фильтрата, Па·с; r – удельное сопротивление осадка, м/кг; с – масса сухого твердого вещества, кг/м3, откладывающегося на фильтре при прохождении через фильтрующую поверхность 1 м3 фильтрата.
| Рис. 7.17. Зависимость Δτ /Δ V от V |  |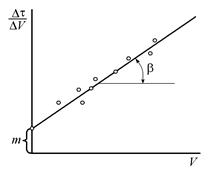
При подстановке значения с в уравнение (7.7) получаем следующую формулу для константы K, м2/с:
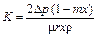. (7.8)
Если известна константа фильтрования K, то удельное сопротивление осадка r может быть найдено по уравнению (7.7), решенному относительно r, м/кг:
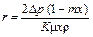. (7.9)
Для инженерных расчетов его можно определить экспериментально по зависимости
r = A (Δ p) n = 6,9·107 ·(Δ p)0,33. (7.10)
Константа фильтрования С, м3/м2, характеризующая сопротивление фильтрующей перегородки (ткани) и отнесенная к 1 м2 площади поверхности фильтра, при Δ р = const определяется следующим выражением:
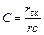(7.11)
или в соответствии с уравнением
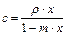, (7.12)
тогда
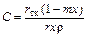, (7.13)
где r тк – удельное сопротивление фильтрующей ткани (на 1 м2 поверхности), м/м2; r – удельное сопротивление осадка, м/кг.
Следовательно, если значение константы фильтрования С известно, то удельное сопротивление ткани может быть вычислено по формуле
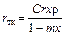. (7.14)
На практике при r / r тк > 103 в расчетах процесса фильтрования r тк опускают.
Тогда уравнение фильтрования принимает вид
V 2 = 2∆ pI 2τ/μ rx. (7.15)
Удельная производительность G уд, кг/(м2 ·ч), может быть получена экспериментально на лабораторной модели фильтра при Δ р = const, набрав необходимую высоту осадка h в течение времени фильтрования τ. Толщина осадка h принимается в соответствии с табл. 7.13.
Объемная производительность фильтра, м3/с, определяется по зависимости
V ф = V уд· F · K п· K м, (7.16)
где V уд – удельная производительность процесса фильтрования, м3/м2 ·ч; F – площадь поверхность фильтрования, м2; K п – поправочный коэффициент, учитывающий увеличение сопротивления фильтрующей перегородки при многократном использовании, K п = 0,8; K м – поправочный коэффициент, учитывающий возможные колебания свойств промышленной суспензии и масштабный переход от лабораторной модели к промышленному фильтру; K м = 0,7…0,9.
Таблица 7.13
Толщина слоя осадка для фильтров
| Фильтр | h min , мм, для слоя | h max , мм | |||
| зернистого, рассыпчатого | проч-ного, мало-влажного | не-прочного, влажного | липкого | ||
| Барабанный с наружной фильтрующей поверхностью Дисковый Ленточный Фильтр-прессы Емкостный ЕдГР-фильтр Механизированный ЕдГр-фильтр | – – – | – – – | – – – | – – – – | – |
Масса сухого вещества G, кг, в осадке при этом составит
G = V ф · с, (7.17)
где V ф – объем фильтрата, м3; с – масса сухого твердого вещества, откладывающегося на фильтре при прохождении через фильтрующую поверхность, кг/м3, определяется экспериментально.
Величина с может быть выражена через концентрацию фильтруемой суспензии х:
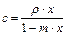, (7.18)
где ρ – плотность фильтрата, кг/м3; x – массовая концентрация твердой фазы в суспензии, кг/кг; m – масса влажного осадка в расчете на 1 кг содержащегося в нем сухого вещества, кг/кг.
Концентрация твердой фазы в суспензии x в зависимости от плотности суспензии ρс выражается формулой
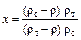. (7.19)
Плотность суспензии находится из выражения
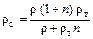, (7.20)
где n – масса жидкой фазы в суспензии в единице массы твердой фазы;
T: Ж = 1: n; n = Ж / Т.
