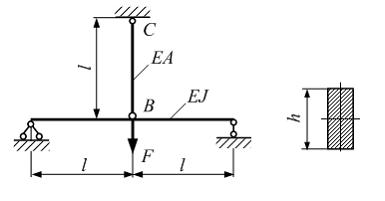
В середине пролета к балке прямоугольного сечения высотой h прикреплен стержень ВС с жесткостью поперечного сечения на растяжение ЕА. Жесткость поперечного сечения балки на изгиб EJ по длине постоянна (J – осевой момент инерции сечения). Линейный размер l задан. Максимальное нормальное напряжение в балке равно … Принять 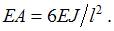
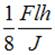 | |||
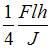 | |||
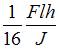 | |||
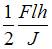 |
Решение:
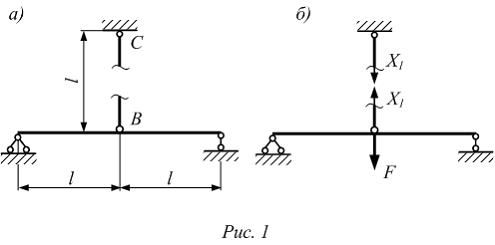
Система один раз статически неопределима. При решении задачи воспользуемся методом сил. Разрезая стержень ВС, получим основную систему (рис. 1а). Эквивалентная система показана на рис. 1 б.
Каноническое уравнение имеет вид
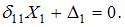
При вычислении коэффициента 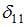 необходимо учесть, влияние не только изгибающих моментов в балке, но и продольной силы в стержне ВС.
необходимо учесть, влияние не только изгибающих моментов в балке, но и продольной силы в стержне ВС.
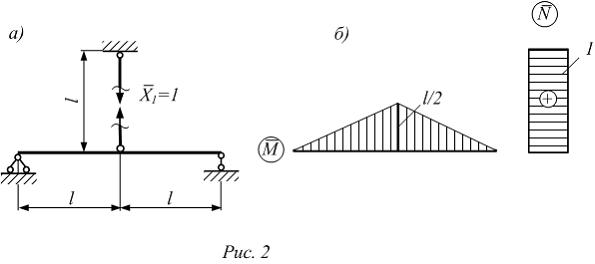
Прикладываем к основной системе единичную силу 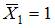 (рис. 2 а). Строим эпюру изгибающих моментов
(рис. 2 а). Строим эпюру изгибающих моментов 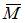 для балки и эпюру продольной силы
для балки и эпюру продольной силы 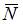 (рис. 2 б) для стержня ВС.
(рис. 2 б) для стержня ВС.
Перемножая эпюру изгибающих моментов 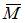 саму на себя по способу Верещагина и, аналогично, эпюру
саму на себя по способу Верещагина и, аналогично, эпюру 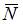 , найдем
, найдем
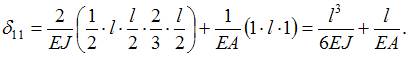
Далее к основной системе прикладываем силу F (рис. 3 а). Строим эпюру изгибающих моментов от заданной силы (рис. 3 б).
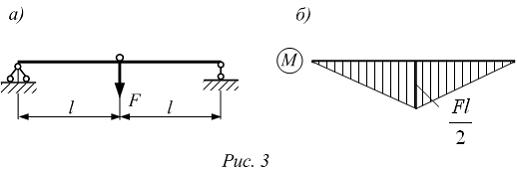
Перемножая эпюры М и 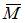 , найдем значение коэффициента
, найдем значение коэффициента 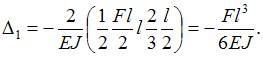
Учитывая, что 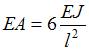 , определим
, определим 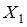
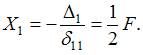
Рассматривая силу 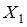 как внешнюю заданную нагрузку (рис. 4 а), построим суммарную эпюру изгибающих моментов для балки (рис. 4 б).
как внешнюю заданную нагрузку (рис. 4 а), построим суммарную эпюру изгибающих моментов для балки (рис. 4 б).
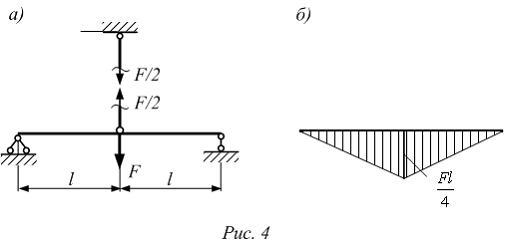
Максимальное нормальное напряжение в балке определим по формуле
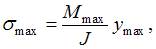
тогда 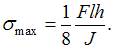
 2015-06-26
2015-06-26 812
812







