ИДЗ №1 ПО ДИСКРЕТНОЙ МАТЕМАТИКЕ
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
ВАРИАНТ 11
Задача 1. Докажите, что при любом натуральном 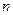 имеет место равенство
имеет место равенство 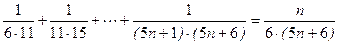 .
.
Задача 2. Докажите, что при любом натуральном 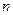
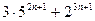 делится на 17.
делится на 17.
Задача 3. Сколько существует различных десятизначных натуральных чисел, состоящих из 5 пятерок, 3 троек и 2 двоек?
Задача 4. Найдите коэффициент при 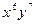 в разложении
в разложении 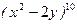 .
.
Задача 5. Даны числовые множества 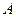 и
и 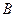 . Найдите
. Найдите 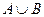 ,
, 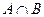 ,
, 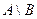 ,
, 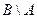 ,
, 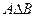 ,
, 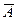 и
и 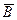 . Изобразите
. Изобразите 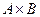 .
.
а) 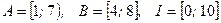 ,
,
б) 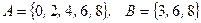 , где
, где 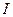 — множество цифр
— множество цифр 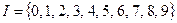 .
.
Задача 6. Каждый из 30 Светиных однокурсников или не пьет, или не курит, или дарит ей цветы. Света выбирает друга, чтоб не пил, не курил и цветы всегда дарил. Известно, что не пьют 18 из них, не курят — 22, дарят цветы — 8; не пьют и не курят 11 человек, не пьют и дарят цветы — 5, не курят и дарят цветы тоже — 5. Сколько у Светы вариантов выбора? Сколько Светиных однокурсников обладают только одним из этих замечательных качеств?
Задача 7. Проверьте, является ли заданное отношение рефлексивным, антирефлексивным, симметричным, антисимметричным, транзитивным, эквивалентным, отношением порядка.
Отношение 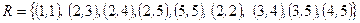 на множестве
на множестве 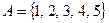 . Запишите матрицу отношения
. Запишите матрицу отношения 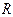 и постройте граф.
и постройте граф.
Задача 8. На множестве действительных чисел задана операция 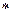 по формуле
по формуле 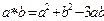 . Проверьте, является ли она коммутативной, ассоциативной.
. Проверьте, является ли она коммутативной, ассоциативной.
Задача 9. Установите взаимно однозначное соответствие между числовыми промежутками 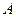 и
и 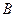 аналитически, если
аналитически, если 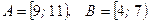 .
.
 2015-06-26
2015-06-26 348
348








