ИДЗ №1 ПО ДИСКРЕТНОЙ МАТЕМАТИКЕ
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
ВАРИАНТ 10
Задача 1. Докажите, что при любом натуральном 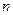 имеет место равенство
имеет место равенство 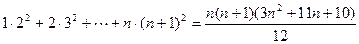 .
.
Задача 2. Докажите, что при любом натуральном 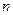
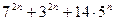 делится на 16.
делится на 16.
Задача 3. Сколькими способами можно распределить 4 разные конфеты между четырьмя девочками, если а) каждая должна получить по конфете, б) разрешаются любые способы распределения?
Задача 4. Найдите коэффициент при 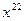 в разложении
в разложении 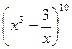 .
.
Задача 5. Даны числовые множества 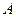 и
и 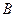 . Найдите
. Найдите 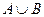 ,
, 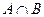 ,
, 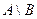 ,
, 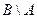 ,
, 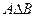 ,
, 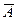 и
и 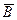 . Изобразите
. Изобразите 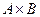 .
.
а) 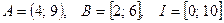 ,
,
б) 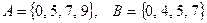 , где
, где 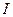 — множество цифр
— множество цифр 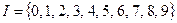 .
.
Задача 6. Три подруги Маша, Даша и Саша решили устроить праздник для своих однокурсников, и каждая составила свой список приглашенных. Оказалось, что у Маши и Саши в списках есть 5 общих друзей, у Даши и у Маши — трое, у Даши и у Саши — только двое, причем один из них есть и в Машином списке. Список Маши был самый длинный — 15 человек, в списке Даши — 7 человек, а у Саши — 10. Сколько гостей оказалось в общем списке? Сколько гостей есть в Машином списке, но нет в Дашином и Сашином?
Задача 7. Проверьте, является ли заданное отношение рефлексивным, антирефлексивным, симметричным, антисимметричным, транзитивным, эквивалентным, отношением порядка.
Отношение 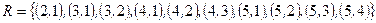 на множестве
на множестве 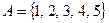 . Запишите матрицу отношения
. Запишите матрицу отношения 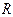 и постройте граф.
и постройте граф.
Задача 8. На множестве действительных чисел задана операция 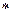 по формуле
по формуле 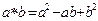 . Проверьте, является ли она коммутативной, ассоциативной.
. Проверьте, является ли она коммутативной, ассоциативной.
Задача 9. Установите взаимно однозначное соответствие между числовыми промежутками 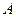 и
и 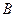 аналитически, если
аналитически, если 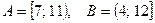 .
.
 2015-06-26
2015-06-26 367
367








