ИДЗ №1 ПО ДИСКРЕТНОЙ МАТЕМАТИКЕ
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
ВАРИАНТ 9
Задача 1. Докажите, что при любом натуральном 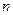 имеет место равенство
имеет место равенство 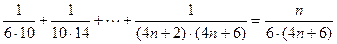 .
.
Задача 2. Докажите, что при любом натуральном 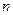
 делится на 25.
делится на 25.
Задача 3. Сколько существует различных последовательностей, состоящих из 10 нулей и 10 единиц?
Задача 4. Найдите коэффициент при 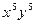 в разложении
в разложении 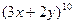 .
.
Задача 5. Даны числовые множества 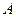 и
и 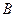 . Найдите
. Найдите 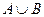 ,
, 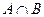 ,
, 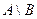 ,
, 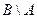 ,
, 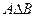 ,
, 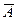 и
и 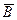 . Изобразите
. Изобразите 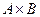 .
.
а) 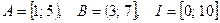 ,
,
б) 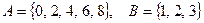 , где
, где 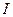 — множество цифр
— множество цифр 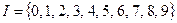 .
.
Задача 6. В клубе почитателей творчества Дэна Брауна организовали экскурсионные туры в Париж, Лондон и Рим по местам действия его романов. Из 40 членов клуба в Париже побывали 25, в Лондоне — 22 и в Риме тоже — 22; В Париже или Лондоне побывало 33 человека, в Париже или Риме — 32, в Лондоне или Риме — 31. Во всех трех городах побывало 10 человек. Сколько членов клуба побывало только в одном из этих городов? Сколько не ездило ни на одну из этих экскурсий?
Задача 7. Проверьте, является ли заданное отношение рефлексивным, антирефлексивным, симметричным, антисимметричным, транзитивным, эквивалентным, отношением порядка.
Отношение 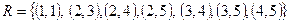 на множестве
на множестве 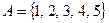 . Запишите матрицу отношения
. Запишите матрицу отношения 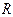 и постройте граф.
и постройте граф.
Задача 8. На множестве действительных чисел задана операция 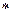 по формуле
по формуле 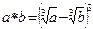 . Проверьте, является ли она коммутативной, ассоциативной.
. Проверьте, является ли она коммутативной, ассоциативной.
Задача 9. Установите взаимно однозначное соответствие между числовыми промежутками 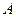 и
и 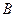 аналитически, если
аналитически, если 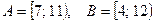 .
.
 2015-06-26
2015-06-26 346
346








