Нормальний розподіл

Нормальним називають розподіл ймовірностей неперервної випадкової величини , якщо диференціальна функція має вигляд

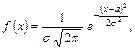
де 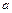– математичне сподівання; 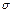– середнє квадратичне відхилення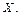

Ймовірність того, що прийме значення, що належить інтервалу ,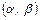

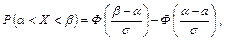
де 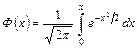– функція Лапласа.

Ймовірність того, що абсолютна величина відхилення менше додатного числа ,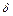

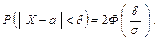
Зокрема, при 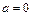справедлива рівність

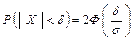
Асиметрія, ексцес, мода та медіана нормального розподілу відповідно дорівнюють:

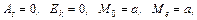
де .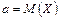

Показовий розподіл
та його числові характеристики

Показовим (експоненціальним) називають розподіл ймовірностей неперервної випадкової величини , який описується диференціальною функцією

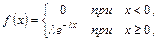
де 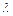– стала додатна величина.

Інтегральна функція показового розподілу

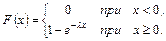
Ймовірність попадання в інтервал 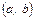неперервної випадкової величини , розподіленої за показовим законом,

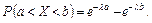
Математичне сподівання, дисперсія та середнє квадратичне відхилення показового розподілу відповідно дорівнюють:

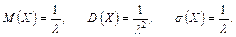
Таким чином, математичне сподівання та середнє квадратичне відхилення показового розподілу дорівнюють між собою.