Розділ 3. Системи двох випадкових величин

Закон розподілу
двовимірної випадкової величини

Двовимірною називають випадкову величину 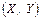, можливі значення якої є пари чисел 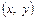. Складові та 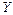, що розглядаються одночасно, утворюють систему двох випадкових величин.

Двовимірну величину геометрично можна витлумачити як випадкову точку 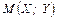на площині 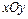, або як випадковий вектор .

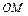Дискретною називають двовимірну величину, складові якої дискретні.

Неперервною називають двовимірну величину, складові якої неперервні.

Законом розподілу ймовірностей двовимірної випадкової величини називають відповідність між можливими значеннями та їх ймовірностями.

Закон розподілу дискретної двовимірної величини може бути заданий: а) у вигляді таблиці з подвійним входом, що містить можливі значення та їх ймовірності; б) аналітично, наприклад, у вигляді інтегральної функції.

Інтегральною функцією розподілу ймовірностей двовимірної випадкової величини називають функцію 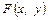, що визначає для кожної пари чисел 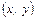ймовірність того, що прийме значення, що менше 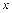, при цьому 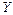прийме значення, що менше :

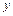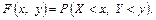
Геометрично цю рівність можна витлумачити так: 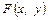є ймовірність того, що випадкова точка 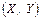потрапить в нескінченний квадрант з вершиною 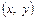, розташований лівіше та нижче цієї вершини.

Часто замість терміна «інтегральна функція» використовують термін «функція розподілу».

Інтегральна функція має наступні властивості:

В л а с т и в і с т ь 1. Значення інтегральної функції задовольняють подвійній нерівності

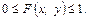
В л а с т и в і с т ь 2. Інтегральна функція є неспадною функцією за кожним аргументом:

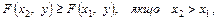
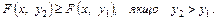
В л а с т и в і с т ь 3. Мають місце граничні співвідношення:

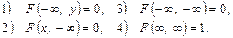
В л а с т и в і с т ь 4.

а) При 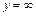інтегральна функція системи стає інтегральною функцією складової :

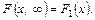
б) При 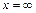інтегральна функція системи стає інтегральною функцією складової :

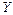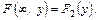
Використовуючи інтегральну функцію, можна знайти ймовірність попадання випадкової точки у прямокутник , :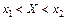

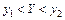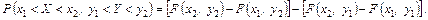
Диференціальною функцією розподілу ймовірностей неперервної двовимірної випадкової величини називають другу змішану похідну від інтегральної функції:

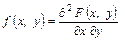
Часто замість терміна «диференціальна функція» використовують термін «двовимірна щільність ймовірності».

Диференціальну функцію можна розглядати як границю відношення ймовірності попадання випадкової точки у прямокутник зі сторонами 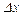та 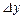до площі цього прямокутника, коли обидві його сторони прямують до нуля; геометрично її можна витлумачити як поверхню, яку називають поверхнею розподілу.

Знаючи диференціальну функцію, можна знайти інтегральну функцію за формулою

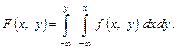
Ймовірність попадання випадкової точки 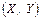в область 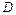визначається рівністю

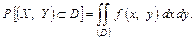
Диференціальна функція має наступні властивості:

В л а с т и в і с т ь 1. Диференціальна функція невід'ємна:

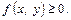
В л а с т и в і с т ь 2. Подвійний невластивий інтеграл з нескінченними границями від диференціальної функції дорівнює одиниці:

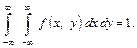
Зокрема, якщо всі можливі значення 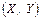належать кінцевій області 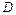, то

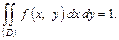
Числові характеристики неперервної системи
двох випадкових величин

Знаючи диференціальні функції складових, можна знайти математичні сподівання та дисперсії:

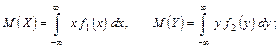
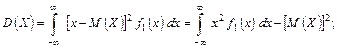
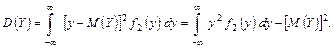
Іноді зручніше використовувати формули, що містять диференціальну функцію системи (подвійні інтеграли беруться по області можливих значень системи):

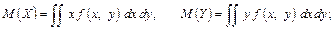
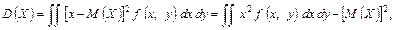
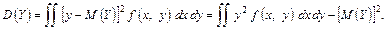
Кореляційним моментом 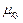системи 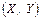називають центральний момент 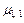порядку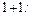

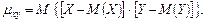
Коефіцієнтом кореляції величин та 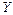називають відношення кореляційного моменту до добутку середніх квадратичних відхилень цих величин:

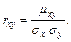
Коефіцієнт кореляції – безрозмірна величина, причому .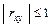

Коефіцієнт кореляції служить для оцінки тісноти л і н і й н о г о зв'язку між та 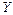: чим ближче абсолютна величина коефіцієнта кореляції до одиниці, тим зв'язок сильніше; чим ближче абсолютна величина коефіцієнта кореляції до нуля, тим зв'язок слабший.

Корельованими називають дві випадкові величини, якщо їх кореляційний момент відмінний від нуля.

Некорельованими називають дві випадкові величини, якщо їх кореляційний момент дорівнює нулю.

Частина 2. ЕЛЕМЕНТИ МАТЕМАТИЧНОЇ СТАТИСТИКИ