2015-06-26
261
а) 78(10) = 4 Е (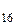 
) = 100 1110 ( 
)
+ + +
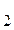47 (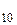 
) = 2 F ( 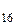) = 10 1111 ( 
)
–––––– –––––– ––––––––––
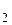125 ( 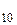) = 7 D ( 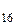)= 111 1101 ( )
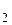б) 1450 ( 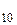)= 5 АА ( 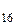) = 101 1010 1010 ( )
– – –
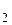427 ( 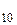)= 1 АВ ( 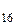) = 1 1010 1011 ( )
–––––– –––––– –––––––––––––
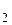1023 ( 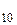)= 3 FF ( 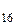) = 11 1111 1111 ( )
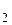В десятичной системе при изображении чисел, больших девяти, различные символы (т. е. цифры 0, 1, …, 9) располагаются друг за другом, например 365. Комбинации этих символов могут быть получены сложением 1 и 0 с последующим добавлением 1 к каждой получаемой сумме: 1 + 0 = 1, 1+ 1 = 2, 1 + 2 = 3 и т. д. Поскольку при операции сложения 1 + 9 сумму невозможно изобразить одним символом, поэтому слева от цифры девять, к которой прибавляется 1, ставится 1, а саму цифру девять заменяют цифрой 0, иначе говоря, осуществляют перенос в старший разряд. После этого можно продолжать операцию добавления 1 к сумме. Описанный процесс, называемый счетом, позволяет получить все комбинации цифр, используемых для изображения чисел в десятичной системе.
• Заметим, что при счете в десятичной системе особое внимание следует обращать на выполнение переноса и замену наибольшей цифры наименьшей.
Рассмотрим теперь, как происходит счет в двоичной системе счисления. Напомним, что в этой системе для изображения чисел используются только два символа: 0 и 1. Начнем счет также, как и в десятичной системе, складывая 1 и 0. Естественно, что 1 + 0 = 1. Добавим к полученной сумме 1. Поскольку сумму в двоичной системе невозможно представить одной цифрой, как и раньше, выполним перенос: припишем слева к первой сумме 1, а ее значение заменим на 0.
• Заметим, что операция переноса выполняется также, как при счете в десятичной системе с той лишь разницей, что в двоичной системе используются только два символа (две двоичные цифры).
В шестнадцатеричной системе счисления используются 16 символов: цифры от 0 до 9 и буквы от А до F. Поэтому шестнадцатеричное число может иметь вид 03 FA. Чтобы определить шестнадцатеричные числа, можно вновь повторить процесс счета подобному тому, как это делалось в случае десятичной и двоичной систем. Сложение и умножение чисел в двоичной, восьмеричной и шестнадцатеричной систем счисления иллюстрируют таблицы 1-6, где по вертикале в первом столбце и по горизонтали в первой строке записаны цифры, на пересечении столбцов и строк результат сложения или умножения.
Таблица 1
Сложение чисел в двоичной системе счисления
| + | ||
Таблица 2
Умножение чисел в двоичной системе счисления
| × | ||
