2015-06-26
250
ПРОЦЕССЫ ПЕРЕНОСА
Когда макросистема находится в равновесии, все ее тер-модинамические параметры постоянны по всему объему сис-темы. Если систему вывести из равновесия и предоставить самой себе, то она постепенно вернется в равновесное сос-тояние. При этом в системе будут протекать необратимые процессы, называемые процессами переноса. Различают нес-колько процессов переноса в зависимости от того, какие па-раметры системы были выведены из равновесия. Это – процессы переноса энергии, плотности и импульса, и свя-занные с ними явления теплопроводности, диффузии и вяз-кости. Процессы переноса возникают, когда имеется гради-ент какого-либо параметра макросистемы по всему объему макросистемы. При этом возникают потоки параметра в сто-рону уменьшения параметра.
Установление равновесия термодинамических систем происходит при помощи движения молекул. Это позволяет получить общее уравнение для всех явлений переноса.
Пусть имеется термодинамическая система с концен-трацией молекул, равной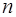 
. Средняя скорость молекул 
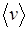. Движение молекул в такой системе будем считать полнос-тью хаотическим для того, чтобы не было направленных то-ков молекул и процессы переноса обусловливались только движением молекул. Возьмем некую площадку 
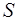единич-ной площади. Определим плотность потока молекул, пере-секающих площадку в одном направлении. Пусть пло-щадка располагается перпендикулярно оси 
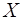. Плотность потока молекул, пересекающих площадку 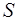в положитель-ном направлении оси 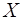будет
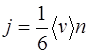. (2.1)
Этот поток и будет переносить физическую величину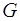 
, выведенную из равновесия, в сторону уменьшения ее значе-ния. Плотность потока величины 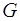обозначим как 
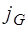. Предположим, что величина 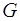характеризует какое-то мо-лекулярное свойство одной молекулы, причем молекула об-ладала этим свойством на расстоянии свободного пробега 
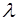от площадки 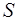. То есть последнее со-ударение молекула испытывала на расстоянии 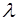от площадки .
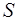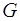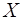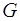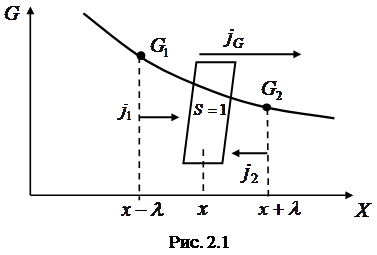
Пусть величина изменяется вдоль оси , т.е. имеет место градиент . Тогда возникает поток величины 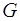в сторону ее уменьшения (рис.2.1).
 |
Тогда общее уравнение переноса для любой величины 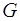через площадку единичной площади, перпендикулярную на-правлению переноса, будет следующим:
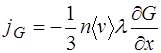, (2.2)
где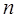 
– концентрация молекул,
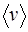– средняя скорость молекул,
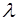– расстояние свободного пробега.
Значения этих величин берутся в сечении 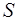. Теперь на основе общего уравнения переноса получим уравнения для переноса массы, импульса и энергии.
