Базис в пространстве и на плоскости
Линейной комбинацией векторов называется  =
= 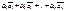
Если существуют такие числа 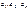 такие, что сумма квадратов их
такие, что сумма квадратов их  0 и произведение
0 и произведение 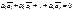 , то вектора
, то вектора 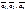 называется линейно зависимыми.
называется линейно зависимыми.
В противном случае вектора называются линейно независимыми
Теорема 1
Два коллинеарных вектора являются линейно зависимыми
Док-ва:
Если  //
//  , то по свойству коллинеарных векторов,
, то по свойству коллинеарных векторов,  =
= 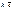 , тогда рассмотрим
, тогда рассмотрим
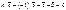 ,
,
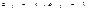
Следствие
Два неколлинеарных вектора на плоскости являются линейно независимыми.
Теорема2
Пусть вектора  и
и  неколлинеарные, тогда любой компланарный им вектор
неколлинеарные, тогда любой компланарный им вектор  представляется единственным образом как их линейная комбинация.
представляется единственным образом как их линейная комбинация.
Док-ва:
На плоскости совместили начала векторов  ,
,  ,
, 
Через концы вектора  проведем прямые, параллельные векторам
проведем прямые, параллельные векторам  и
и 
Получили параллелограмм по свойству суммы векторов  =
= 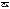 +
+ 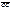
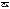 //
//  ,
, 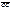 //
// 
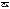 =
= 
 ,
, 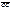 =
= 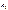

 =
= 
 +
+ 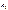

 вектор
вектор  - это линейная комбинация векторов
- это линейная комбинация векторов  и
и 
Докажем, что  представляется единственным образом
представляется единственным образом
Пусть существует еще одна линейная комбинация, соответствующая вектору 
0 = 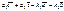
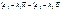 , т.к. вектора
, т.к. вектора  и
и 
 0
0  сумма будет = 0, если
сумма будет = 0, если 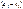 ,
, 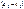 = 0
= 0 
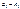 ,
, 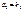
 2015-06-28
2015-06-28 218
218







