Відстань від точки до прямої

Дано загальне рівняння прямої

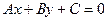(17)

і точку 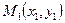. Знайдемо відстань 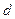від точки 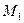до прямої (17). Візьмемо точку 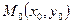на цій прямій.

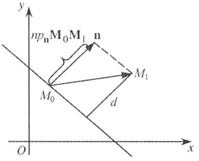Тоді відстань від точки 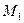до прямої дорівнює проекції вектора 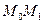на вектор нормалі 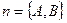(рис. 7)

Рис. 7

Записуємо аналітичний вираз для шуканої відстані:

.

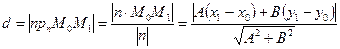Оскільки 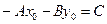, то остаточно маємо:

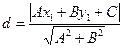. (18)

Означення. Рівняння виду

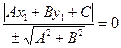(19)

називається нормальним рівнянням прямої (17). Знак перед радикалом має бути протилежний знаку вільного члена 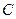. Якщо 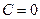, то вибір знака значення не має.

Узявши в нормально рівнянні (19)

, , ,

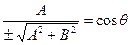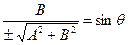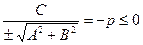запишемо його у вигляді 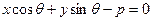, де 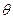– кут між віссю 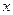і вектором нормалі 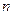; 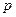– відстань від прямої до початку координат (рис. 8).

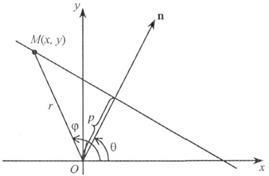
Рис. 8

Перейдемо до полярних координат, скориставшись рівностями 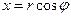, 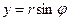. Тоді Нормальне рівняння прямої набере вигляду

.

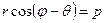Залежність, записану формулою (18), можна сформулювати як теорему.

Теорема 3. Для того щоб знайти відстань 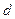від точки 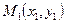до прямої, заданої рівнянням (17), достатньо підставити координати точки 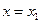, 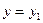у нормальне рівняння прямої і знайти модуль здобутої величини.