Розглянемо на площині прямокутну систему координат 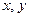 і знайдемо рівняння прямої, коли відомий вектор її нормалі
і знайдемо рівняння прямої, коли відомий вектор її нормалі 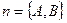 і задано точку
і задано точку 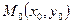 на цій прямій. Нехай
на цій прямій. Нехай 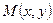 – довільна точка шуканої прямої (рис. 5).
– довільна точка шуканої прямої (рис. 5).
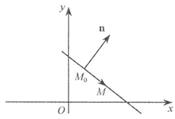
Рис. 5.
За умовою вектор 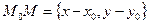 перпендикулярний до вектора
перпендикулярний до вектора 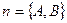 . Тому їх скалярний добуток
. Тому їх скалярний добуток 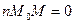 . Звідси маємо рівняння
. Звідси маємо рівняння
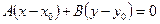 (11)
(11)
або
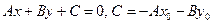 (12)
(12)
Це рівняння називається загальним рівнянням прямої.
На відміну від рівняння виду (11) змінні 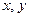 входять до рівняння (12) рівноправно. Рівняння (11) завжди можна подати у вигляді (12).
входять до рівняння (12) рівноправно. Рівняння (11) завжди можна подати у вигляді (12).
Рівняння прямої (12) можна записати у вигляді 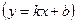 лише за умови
лише за умови 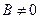 .
.
Коефіцієнт 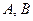 при
при 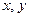 у загальному рівнянні прямої є проекціями на координатні осі вектора її нормалі
у загальному рівнянні прямої є проекціями на координатні осі вектора її нормалі 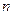 .
.
Спавджується теорема.
Теорема 1. Будь-яка пряма на площі може бути задана лінійним рівнянням виду (12). Кожне лінійне рівняння виду (12), де 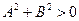 , визначає деяку пряму.
, визначає деяку пряму.
Нехай 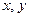 – координати довільної точки на площині. Пряма (12) поділяє свою площину на дві півплощини. В одній півплощині виконується нерівність
– координати довільної точки на площині. Пряма (12) поділяє свою площину на дві півплощини. В одній півплощині виконується нерівність 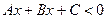 . На самій прямій маємо:
. На самій прямій маємо: 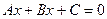 .
.
Розглянемо частинні випадки рівняння (12):
Ø якщо 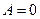 , то пряма паралельна осі
, то пряма паралельна осі 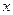 ;
;
Ø якщо 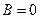 , то пряма паралельна осі
, то пряма паралельна осі 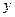 ;
;
Ø якщо 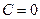 , то пряма проходить через початок координат;
, то пряма проходить через початок координат;
Ø якщо 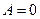 ,
, 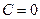 , то пряма збігається з віссю
, то пряма збігається з віссю 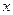 ;
;
Ø якщо 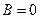 ,
, 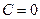 , то пряма збігається з віссю
, то пряма збігається з віссю 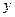 .
.
Нагадаємо, що пряма проходить перпендикулярно до вектора 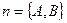 .
.
 2015-06-28
2015-06-28 1611
1611








