Для построения графиков функций, содержащих выражения под знаком модуля сначала находят корни выражений, стоящих под знаком модуля. Эти корни разбивают числовую прямую на промежутки. График строят в каждом промежутке отдельно.
В случае, когда только одно выражение стоит под знаком модуля и нет слагаемых без знака модуля, можно построить график функции, опустив знак модуля, а затем часть графика, расположенную в области отрицательных значений у, отобразить симметрично относительно оси О х. Это вытекает из определения модуля числа.
Пример 1. Постройте график функции у = 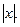
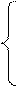 Решение: По определению модуля числа имеем:
Решение: По определению модуля числа имеем:
а, если а 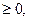
| а | =
- а, если а < 0.
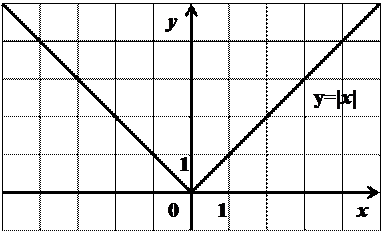
Используя график функции 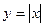 , постройте график функции:
, постройте график функции:
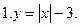


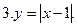
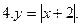
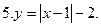
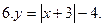
7. у = 1 - 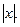 8. у = 2 -
8. у = 2 - 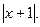
9. у = 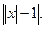 10. у =
10. у = 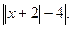
11. у = 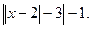 12. у =
12. у = 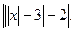
13. у = 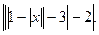 14. у =
14. у = 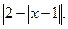
15. у = 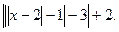 16. у =
16. у = 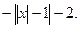
Пример 2. Постройте график функции: у = 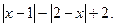
Решение: х – 1 = 0; 2 – х = 0;
х = 1. х = 2.
1) х < 1: у = - х + 1 – 2 + х + 2, у = 1.
2) 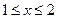 : у = х – 1 – 2 + х + 2, у = 2 х – 1.
: у = х – 1 – 2 + х + 2, у = 2 х – 1.
3) х > 2: у = х – 1 + 2 – х +2, у = 3.
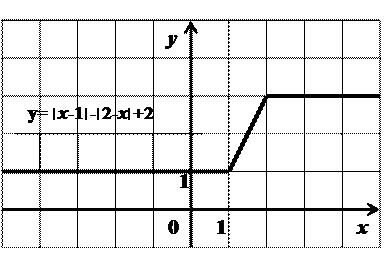
Постройте график функции:
|
|
|
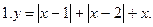
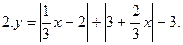
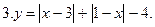
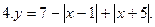
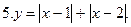
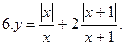
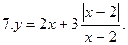
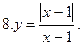
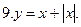
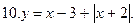
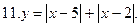
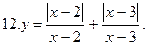
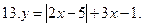
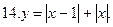
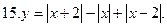

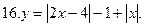
Постройте график уравнения:
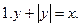
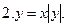
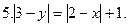
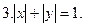
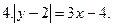
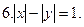

Пример 3. Постройте график функции: 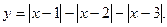
Решение: Графиком функции является ломаная линия с вершинами в точках с абсциссами х = 1, х = 2, х = 3. Найдём ординаты этих точек:
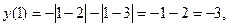
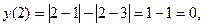
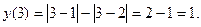
Значит, вершинами ломаной являются точки: (1;-3), (2;0), (3;1). Используя ещё две дополнительные точки (0;-4) и (4;0), строим график функции.
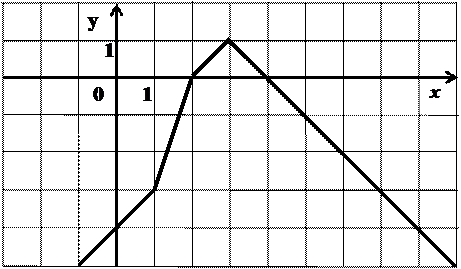
Постройте график функции:
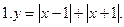
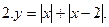
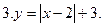
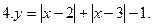
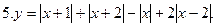
 2015-06-28
2015-06-28 405
405








