СЕЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ТЕЛ ПЛОСКОСТЬЮ
В заданиях на построение усеченных геометрических тел можно выделить следующие задачи: 1) построение усеченного тела в системе трех плоскостей проекций; 2) определение истинной величины фигуры сечения; 3) построение развертки усеченного тела и 4) вычерчивание его аксонометрической проекции. Ниже помещены рекомендации по решению каждой из перечисленных задач.
Вначале по положению секущей плоскости определяют вид фигуры сечения и в зависимости от формы геометрического тела выбирают прием построения проекций сечения. В заданиях секущие плоскости занимают проецирующее положение, поэтому одна проекция сечения задается. Недостающие проекции фигуры сечения призмы или пирамиды строят по точкам пересечения их ребер с заданной плоскостью. Если же плоскость пересекает поверхность вращения по лекальной кривой, то начинают с определения ее характерных точек.
Например, фронтально проецирующая плоскость Р (рис. 106) пересекает цилиндр по неполному эллипсу. Его характерными точками являются: 1) А и В — точки, принадлежащие линии пересечения плоскости Р с основанием цилиндра; 2) С — конец большой оси эллипса; 3) D и Е — концы малой оси эллипса и они же точки, лежащие на очерковых образующих цилиндра Последовательность нахождения точек эллипса указана стрелками на примере промежуточных точек 1 и 2.
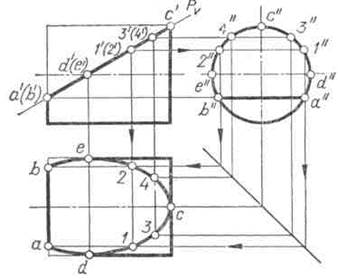
Рис. 106
Истинную величину фигуры сечения определяют с помощью способа перемены плоскостей проекций или вращения. Если применяют способ перемены плоскостей проекций, то дополнительную плоскость задают параллельно секущей плоскости. Дополнительную плоскость совмещают с основной плоскостью проекций так, чтобы новая проекция сечения не наложилась на имеющиеся проекции. При использовании способа вращения ось вращения целесообразно располагать в секущей плоскости и на некотором расстоянии от тела.
Для примера показано положение оси вращения U (рис. 107) при определении истинной величины сечения четырехугольной призмы фронтально проецирующей плоскостью Р.
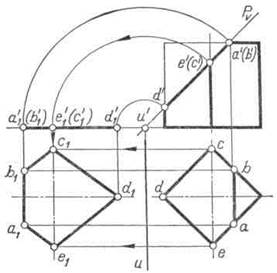
Рис. 107
Построение развертки усеченного тела начинают с вычерчивания развертки его полной боковой поверхности. Далее на нее наносят линии сечения и пристраивают к ней остальные части развертки — основания и фигуру сечения. Если какие-либо элементы, необходимые для построения развертки, на проекциях искажены, то предварительно определяют их истинную величину.
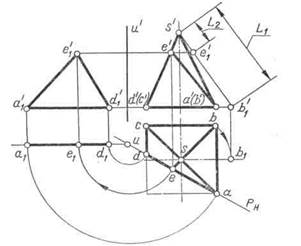
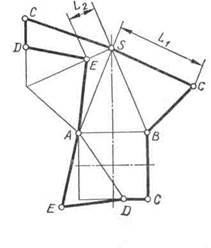
Рис. 108
Например, для построения развертки правильной усеченной четырехугольной пирамиды (рис. 108) необходимо определить истинную величину фигуры сечения — треугольника ADE и длину одного из ее боковых ребер, например ребра SB. Для определения истинной величины этих элементов их поворачивают до положения, параллельного плоскости V. Треугольник ADE повернут вокруг оси U, а ребро SB — вокруг высоты пирамиды. Далее строят развертку согласно рекомендациям в следующем порядке: задают положение вершины S; вычерчивают развертку полной боковой поверхности пирамиды; наносят на нее линии сечения DE и AE с помощью отрезков SE = = s′e′1 = L2 и DC = dc; пристраивают к ребру основания АВ фигуру усеченного основания— четырехугольник ABCD = abcd и к его стороне AD — треугольник ADE = a′1e′1 d′1.
Усеченные тела на аксонометрической проекции вначале вычерчивают целыми. Далее изображают проекцию сечения и контурными линиями обводят усеченную часть тела.
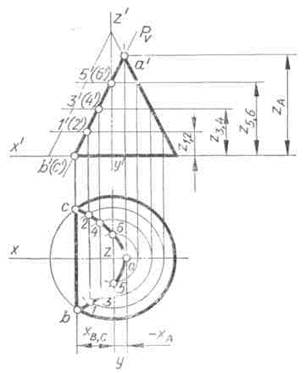
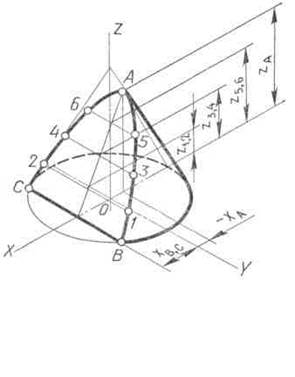
Рис. 109
Для примера на рис. 109 вычерчена изометрическая проекция конуса, усеченного фронтально проецирующей плоскостью Р по параболе. Параболу на изометрической проекции начинают строить с ее вершины А. Эту точку получают с помощью координаты— хА. Проекции нижних точек параболы В и С строят по координате хВ, С. Соединив точку А с серединой отрезка ВС, получают проекцию оси симметрии параболы. Для построения ее промежуточных точек откладывают по оси конуса от его основания отрезки, равные координатам z1,2, z3,1, z5,6. Через концы отложенных отрезков проводят прямые, параллельные оси координат X, до пересечения с осью симметрии параболы. Через полученные точки проводят хорды параболы, которые параллельны ее нижней хорде ВС. Длину каждой хорды замеряют на горизонтальной проекции усеченного конуса и откладывают на соответствующей хорде изометрической проекции.
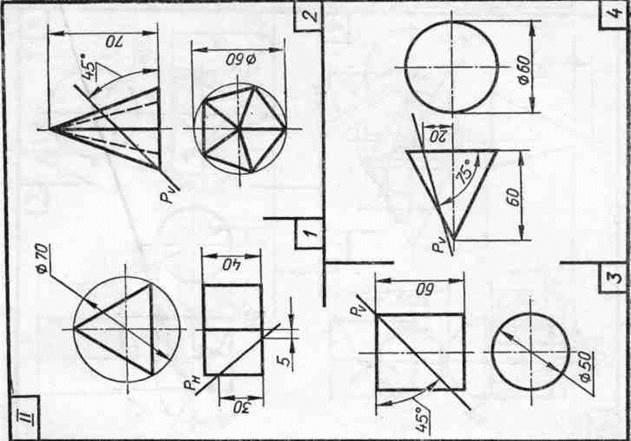
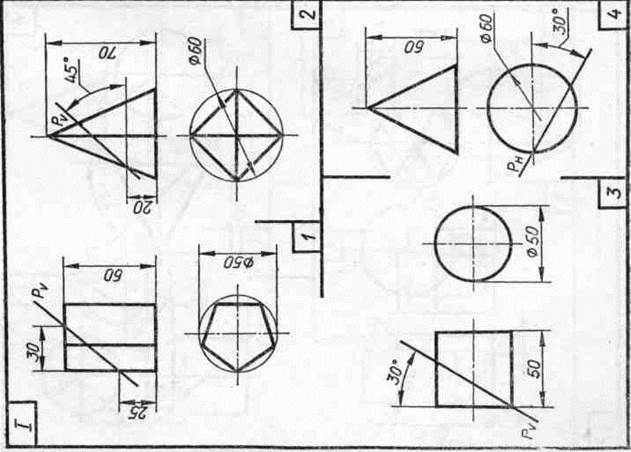
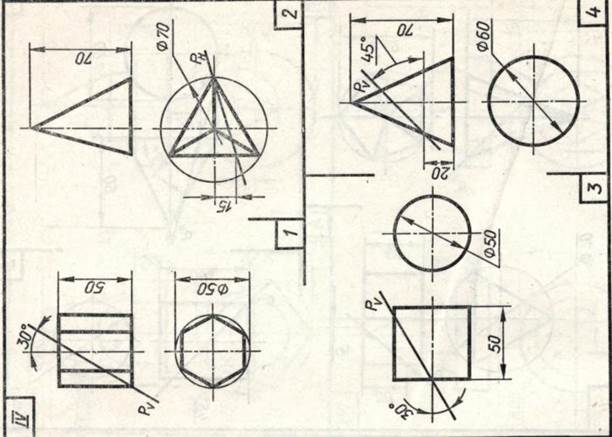
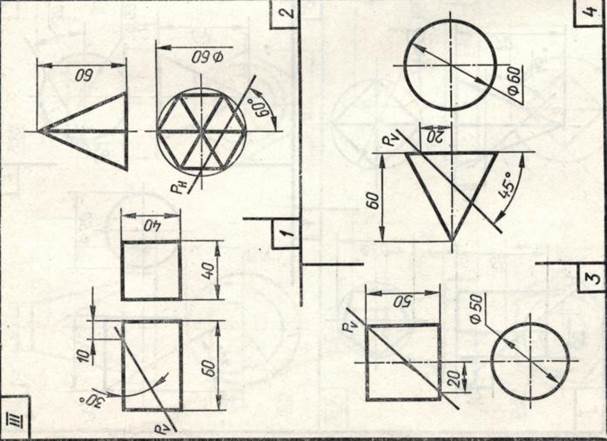
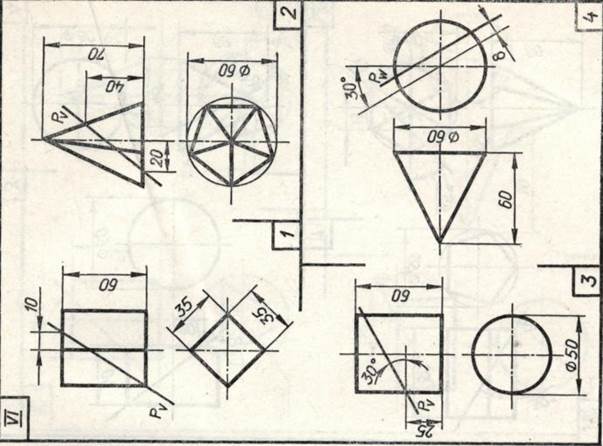
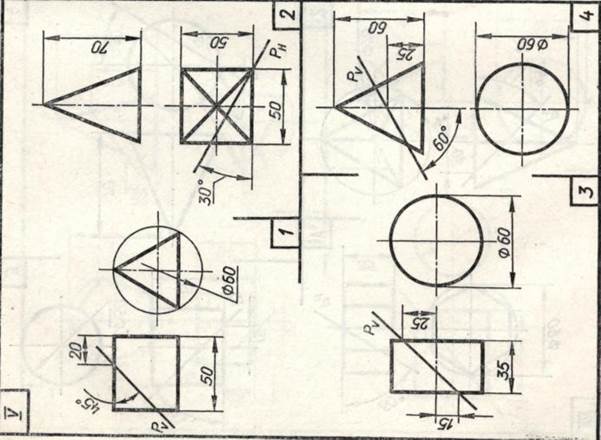
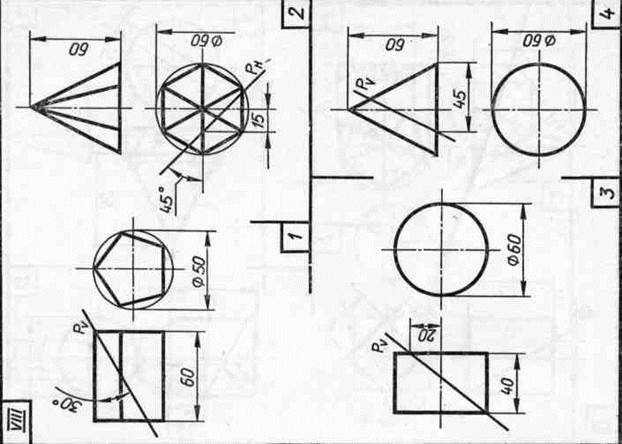
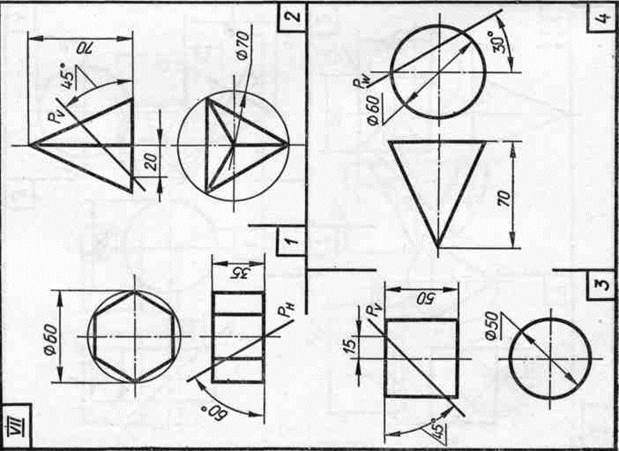
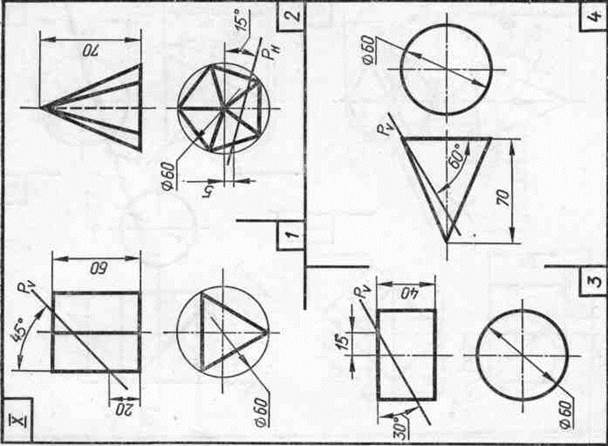
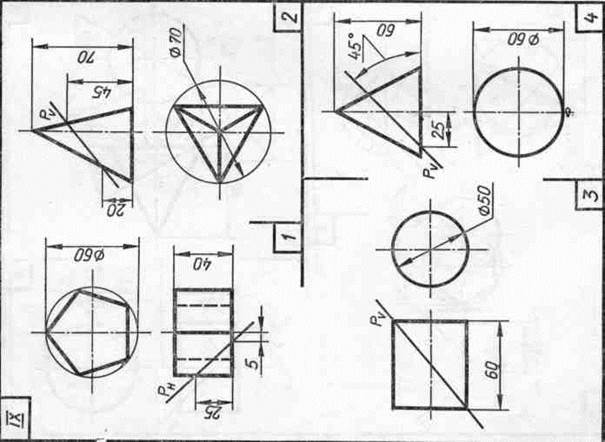
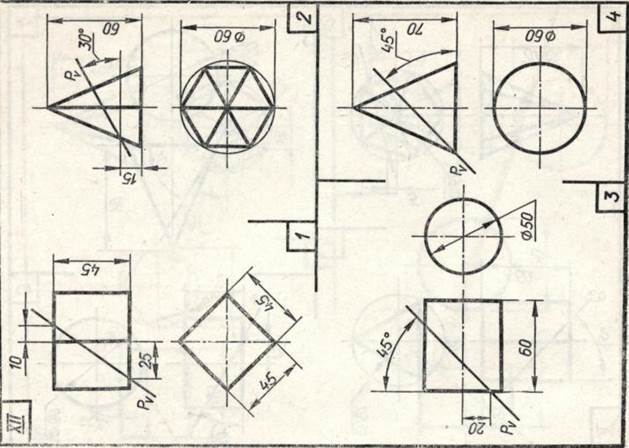
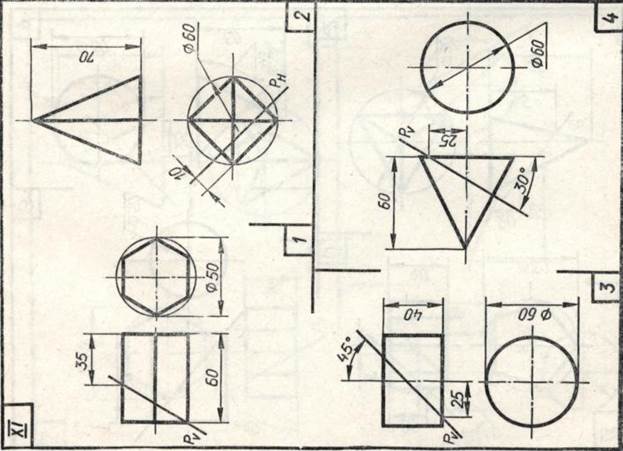
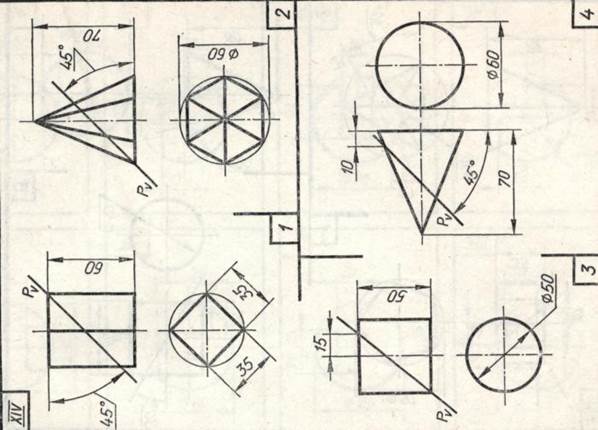
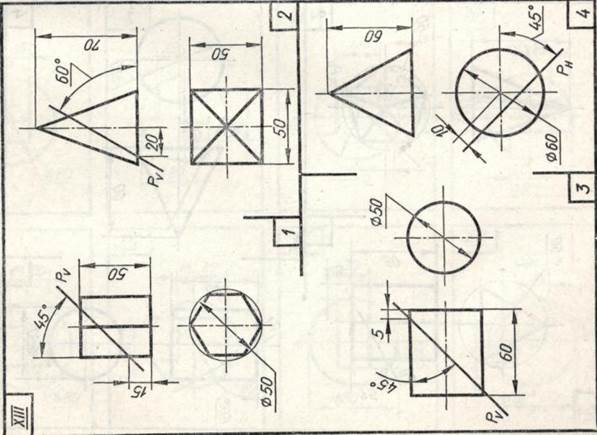
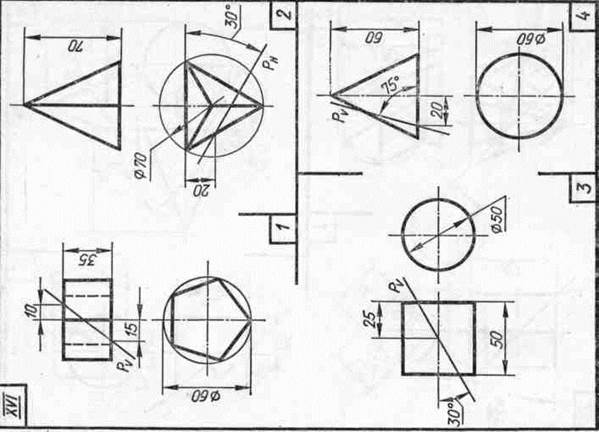
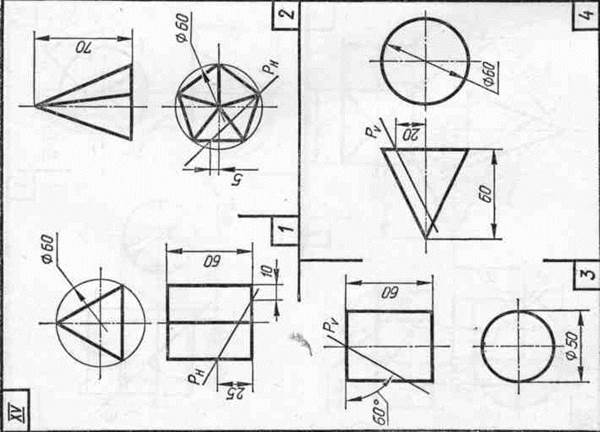
Задание 23. Усеченные геометрические тела. Построить заданные усеченные геометрические тела (призму, пирамиду, цилиндр, конус) в системе трех плоскостей проекций, определить истинные величины фигур сечения, вычертить развертки усеченных тел и их аксонометрические проекции. Вид аксонометрической проекции указан в табл. 13.
Таблица 13
| Варианты задания | Прямоугольная изометрическая проекция | Прямоугольная диметрическая проекция |
| номера задач | ||
| I, III, V, VII, IX, XI, XIII, XV | 1, 3 | 2, 4 |
| II, IV, VI, VIII, X, XII,XIV | 2, 4 | 1, 3 |
| XVI | 1, 4 | 2, 3 |
Изображение каждого геометрического тела располагают на листе формата A3.
Образцы выполненного задания с разными вариантами оформления приведены на рис. 110—113.
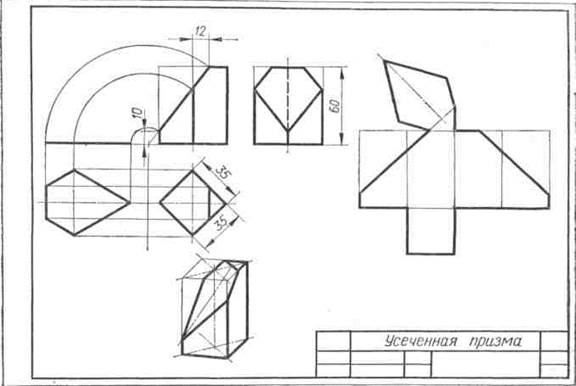
Рис.110
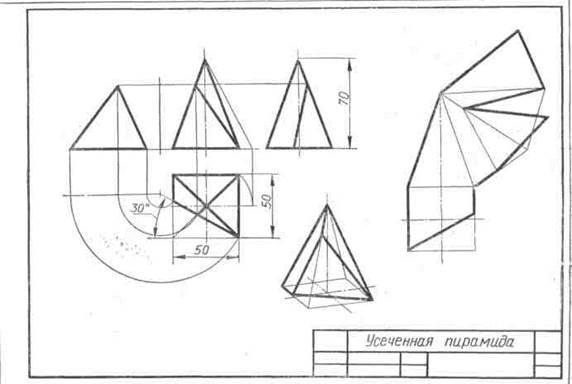
Рис. 111
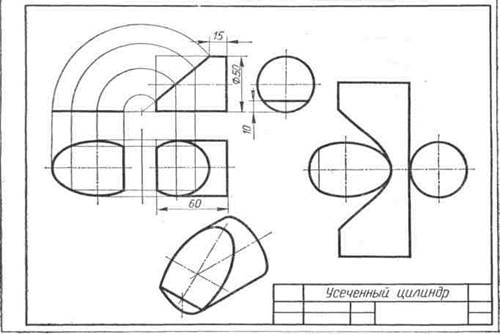
Рис. 112
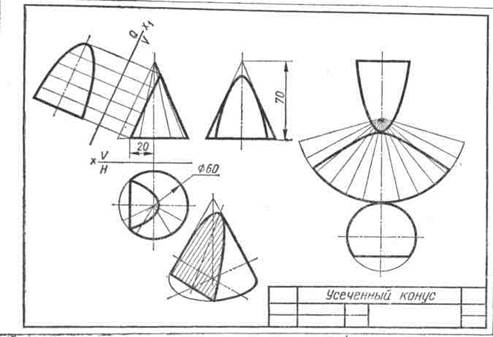
Рис. 113
Работу над заданием следует начинать с компоновки чертежа, которая довольно трудоемка из-за большого количества изображений. Габариты горизонтальной, фронтальной, профильной и аксонометрической проекций тела подсчитывают по заданным проекциям. Размеры сечения и развертки определяют приблизительно или делают на черновике нужные построения.
Сократить работу с предлагаемым заданием можно, уменьшив число геометрических тел или упростив содержание задания. Например, отказаться от вычерчивания аксонометрической проекции тела или не строить его развертку.
 2015-06-28
2015-06-28 21473
21473