Точку пересечения прямой линии 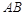 общего положения с плоскостью
общего положения с плоскостью 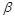 общего положения строят в следующем порядке:
общего положения строят в следующем порядке:
а) через заданную прямую 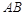 проводят вспомогательную плоскость
проводят вспомогательную плоскость 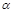 ;
;
б) строят линию пересечения 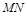 вспомогательной плоскости
вспомогательной плоскости 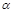 и заданной плоскости
и заданной плоскости 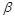 ;
;
в) в пересечении линии 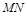 с заданной прямой
с заданной прямой 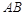 отмечают искомую точку
отмечают искомую точку 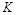 .
.
На рис.28 показано построение точки пересечения 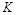 прямой
прямой 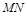 с плоскостью общего положения
с плоскостью общего положения 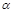 , заданной треугольником
, заданной треугольником 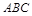 . Здесь применяется горизонтально-проецирующая плоскость
. Здесь применяется горизонтально-проецирующая плоскость 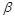 , которая пересекает треугольник
, которая пересекает треугольник 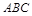 по прямой
по прямой 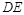 . Считая, что в пространстве заданы прямая и непрозрачный треугольник, определяем видимые и невидимые части прямой
. Считая, что в пространстве заданы прямая и непрозрачный треугольник, определяем видимые и невидимые части прямой 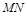 относительно плоскостей
относительно плоскостей 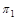 и
и 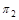 .
.
Зоны видимости поясним исходя из положения точек на скрещивающихся прямых. Так в точке 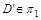 совмещаются горизонтальные проекции двух точек
совмещаются горизонтальные проекции двух точек 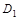 и
и 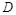 (
(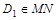 ,
, 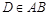 ,смотрим сверху вниз), и так как
,смотрим сверху вниз), и так как 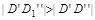 , то в горизонтальной проекции на участке
, то в горизонтальной проекции на участке 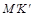 - прямая видимая, а
- прямая видимая, а 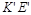 - невидимая. Для определения видимости во фронтальной плоскости смотрим снизу вверх: в точке
- невидимая. Для определения видимости во фронтальной плоскости смотрим снизу вверх: в точке 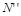 совпадают фронтальные проекции точек
совпадают фронтальные проекции точек 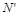 и
и 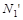 ;
; 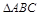 закрывает прямую
закрывает прямую 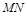 (
(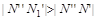 ), поэтому
), поэтому 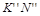 будет невидимой во фронтальной проекции, а
будет невидимой во фронтальной проекции, а 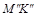 - видимой частью проекции
- видимой частью проекции 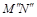 .
.
Для построения линии пересечения плоскостей строят точки пересечения прямых одной плоскости с другой и через них проводят искомую линию.
Способы преобразования чертежа. Способ перемены плоскостей проекций.
Способ вращения.
Решение задач способами начертательной геометрии сводится к определению позиционных и метрических характеристик геометрических фигур. Рассматриваются:
Задачи позиционные – решение задач этой группы должно дать ответ на вопрос о взаимном расположении геометрических фигур.
Задачи метрические – при решении задач этой группы появляется возможность ответить на вопросы, касающихся как внутренней метрики заданных геометрических фигур (определение расстояний, нахождение углов), так и определение расстояний между точками и величин углов между линиями различных фигур.
Многие задачи решаются легко и просто, если геометрические фигуры находятся в частном положении. Рассмотрим основные способы преобразования чертежа общего положения в частное положение:
1) Первый способ - заменяют заданную систему плоскостей проекций на новую так, чтобы в ней исходные объекты оказались в частном положении, не меняя своего положения в пространстве (способ перемены плоскостей проекций);
2) Второй способ - изменяют положение исходных объектов в пространстве так, чтобы они приняли частное положение относительно неизменных плоскостей проекций (способ вращения).
Сущность способа перемены плоскостей проекций заключается в том, что положение точек, линий, плоских фигур, поверхностей в пространстве остается неизменным, а система 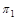 ,
, 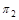 дополняется плоскостями, образующими с плоскостью
дополняется плоскостями, образующими с плоскостью 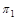 или
или 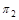 , или между собой системы двух взаимно перпендикулярных плоскостей, принимаемых за плоскости проекций.
, или между собой системы двух взаимно перпендикулярных плоскостей, принимаемых за плоскости проекций.
Каждая новая перпендикулярная система выбирается так, чтобы по отношению к заданным геометрическим элементам она заняла положение наиболее удобное для выполнения требуемого задания. При введении новой плоскости проекций, ось проекций будет обозначаться в виде дроби, черта которой лежит на оси, а обозначения плоскостей проекций представляют собой как бы числитель и знаменатель дроби, причем каждая буква ставится по ту сторону оси, где должны размещаться соответствующие проекции. Перемену плоскостей проекций можно производить последовательно несколько раз. Номер плоскости обозначает количество штрихов у проецируемых букв.
Выделим пять основных задач преобразования.
1 Определение величины отрезка 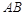 общего положения и угла наклона к плоскости проекций приведено на рис.1. Натуральная величина
общего положения и угла наклона к плоскости проекций приведено на рис.1. Натуральная величина 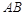 равна
равна 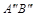 ,
, 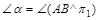 .При построении равные отложенные расстояния отмечены соответствующими значками.
.При построении равные отложенные расстояния отмечены соответствующими значками.
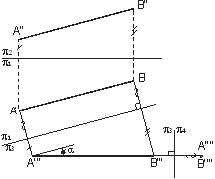
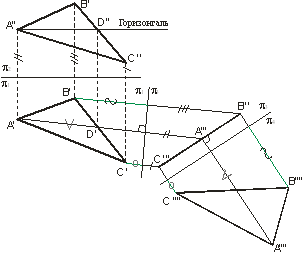
Рис.1 Рис.2
2 Приведение отрезка прямой общего положения в проецирующее положение изображено на рис.1. Чтобы заданную в системе 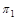 ,
, 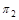 прямую общего положения
прямую общего положения 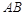 , расположить перпендикулярно к дополнительной плоскости проекций, необходимо введение двух дополнительных плоскостей проекций.
, расположить перпендикулярно к дополнительной плоскости проекций, необходимо введение двух дополнительных плоскостей проекций.
3 Приведение плоской фигуры общего положения в проецирующее положение и угла между данной плоскостью и плоскостью проекций. На рис.2 это осуществлено с помощью горизонтали, а на рис.3 – с помощью фронтали. На рис.3 определен 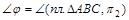
4 Определение натурального вида плоской фигуры, расположенной в проецирующем положении. Пример построения натурального вида 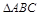 дан на рис.2.
дан на рис.2.
5 Определение расстояния между скрещивающимися прямыми.
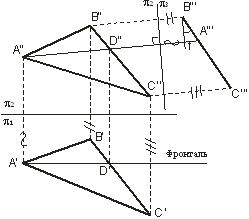
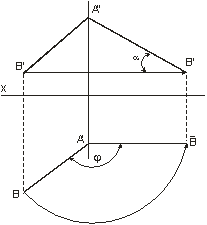
Рис.3 Рис.4
При вращении некоторой точки вокруг оси она движется в плоскости вращения, перпендикулярной оси вращения, и описывает окружность некоторого радиуса. В качестве оси вращения обычно используются прямые перпендикулярные или параллельные плоскости проекции.
При вращении точки вокруг вертикальной оси ее горизонтальная проекция перемещается по окружности, а фронтальная проекция – параллельно оси х. Если точку вращения вокруг оси перпендикулярной плоскости 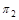 , то ее фронтальная проекция будет перемещаться по окружности, а горизонтальная проекция - на плоскости
, то ее фронтальная проекция будет перемещаться по окружности, а горизонтальная проекция - на плоскости 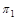 в виде отрезка прямой линии параллельно оси х.
в виде отрезка прямой линии параллельно оси х.
Вращение вокруг проецирующей прямой применяют когда надо найти натуральную величину отрезка прямой и угол ее наклона. На рис.4 вращая точку В на угол 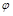 в положение
в положение 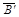 , так, что
, так, что 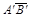 параллельно плоскости
параллельно плоскости 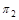 , определяется величина отрезка AB, равная
, определяется величина отрезка AB, равная 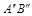 и угол
и угол 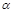 с плоскостью
с плоскостью 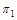 , здесь плоскости вращения перпендикулярны плоскости
, здесь плоскости вращения перпендикулярны плоскости 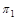 и проходят через точку А поэтому точка А остается неподвижной.
и проходят через точку А поэтому точка А остается неподвижной.
Натуральную величину плоской фигуры можно определить вращением вокруг оси, параллельной плоскости проекции, одним поворотом приведя фигуру в положение, параллельное плоскости проекции.
Изображение многогранников. Чертежи призм и пирамид.
Пересечение призм и пирамид прямой линией и плоскостью.
Грани призм и пирамид ограничиваются ребрами, являющимися прямоугольными отрезками, пересекающимися между собой. Поэтому построение чертежей призм и пирамид сводится к построению проекций вершин (точек) и ребер (отрезков прямых).
На чертеже основание призмы (рис.1 и рис.2) обычно размещают параллельно плоскости проекций, а одноименные проекции ее ребер параллельны между собой. Признаками того, что на чертеже изображена призма является наличие на чертеже только прямолинейных отрезков, причем они служат проекциями ребер или граней, наличие параллелограммов или прямоугольников как проекций боковых граней и любого многоугольника как проекции основания.
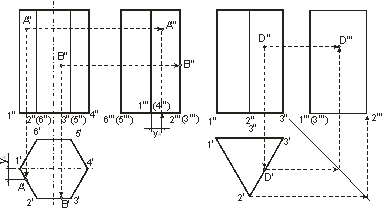
Рис.1 Рис.2
Грани призм и пирамид, которые перпендикулярны к плоскостям проекций, проецируются на них в виде отрезков прямых линий. Недостающие проекции точек на поверхности призм и пирамид по заданным фронтальным проекциям строят по их принадлежности ребрам (прямым линиям) и граням (плоскостям). На рис.1 и 2 их построение показано стрелками и соответствующими обозначениями.
На чертеже пирамиду задают проекциями ее оснований, ребер и вершин (рис.3 и рис.4). Для усеченной пирамиды необходимо указывать проекции обоих оснований.
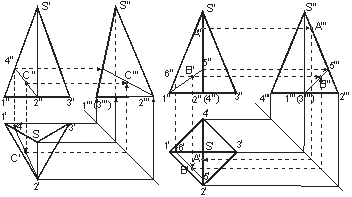
Рис.3 рис.4
Изображая пирамиду, ее основание обычно располагают параллельно плоскости проекций. Построение проекций точек на других плоскостях на чертежах показано линиями проекций со стрелками. Горизонтальная 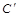 и профильная
и профильная 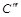 проекции точки С на грани
проекции точки С на грани 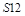 построены (рис.3) с помощью проекций
построены (рис.3) с помощью проекций 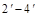 и
и 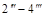 этой грани. Аналогично, с помощью профильной проекции
этой грани. Аналогично, с помощью профильной проекции 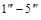 на грани
на грани 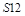 пирамиды (рис.4) построена профильная проекция
пирамиды (рис.4) построена профильная проекция 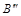 . Горизонтальная проекция
. Горизонтальная проекция 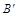 построена с помощью горизонтали
построена с помощью горизонтали 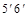 той же грани (
той же грани (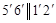 ).
).
При пересечении поверхности призмы (рис.5) или пирамиды (рис.6) прямой линией получается две точки: точка входа и точка выхода. Чтобы найти эти точки надо провести через данную прямую вспомогательную плоскость и найти линии ее пересечения с гранями: эти линии на гранях оказываются расположенными в одной плоскости с данной прямой и в своем пересечении дают искомые точки. На рис.5 дополнительная плоскость не нужна, так как решение очевидно. На рис.6 через 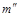 проводится вспомогательная плоскость b — фронтально-проецирующая, сначала определяются проекции
проводится вспомогательная плоскость b — фронтально-проецирующая, сначала определяются проекции 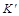 ,
, 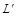 (как точки пересечения
(как точки пересечения 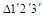 с проекцией
с проекцией 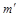 ), а затем – по линиям связи определяются проекции
), а затем – по линиям связи определяются проекции 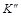 ,
, 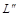 учитывая элементы видимости.
учитывая элементы видимости.
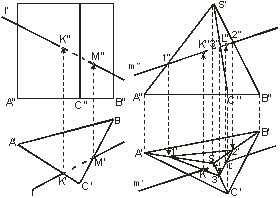
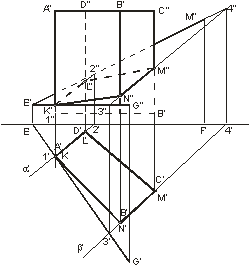
Рис.5 Рис.6 Рис.7
При пересечении призмы или пирамиды плоскостью в сечении получается плоская фигура, ограниченная линиями пересечения секущей плоскости с гранями призмы или пирамиды.
Для построения фигуры, получаемой при пересечении призмы и пирамиды плоскостью, надо или найти точки, в которых ребра призмы или пирамиды пересекают данную плоскость, или найти отрезки прямых, по которым грани призмы или пирамиды пересекаются плоскостью. В первом случае построение сводится к задаче на пересечение прямой с плоскостью, во втором случае – на пересечение плоскостей между собой.
В тех случаях, когда секущая плоскость не параллельна ни одной из плоскостей проекций, фигура сечения проецируется с искажением. Поэтому, если требуется определить натуральный вид фигуры сечения, то следует применять один из способов, которые позволяют находить длину отрезка, величину угла и т.д..
На рис.7 четырехугольная призма пересекается плоскостью 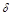 = (EF,EG). При пересечении получается четырех угольник KLMN, вершины которого представляют собой точки пересечения ребер призмы с плоскостью
= (EF,EG). При пересечении получается четырех угольник KLMN, вершины которого представляют собой точки пересечения ребер призмы с плоскостью 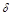 . Горизонтальная проекция фигуры сечения совпадает с
. Горизонтальная проекция фигуры сечения совпадает с 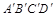 , так как призма прямая и основание ее параллельно плоскости
, так как призма прямая и основание ее параллельно плоскости 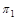 . Точки K и L находятся с помощью дополнительной плоскости
. Точки K и L находятся с помощью дополнительной плоскости 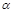 , которой принадлежит грань AD призмы. Проведя плоскость
, которой принадлежит грань AD призмы. Проведя плоскость 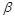 , получим 3 – 4 и точки
, получим 3 – 4 и точки 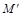 и
и 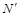 . Эти плоскости пересекаются с данной плоскостью по отрезкам KL и NM.
. Эти плоскости пересекаются с данной плоскостью по отрезкам KL и NM.
На фронтальной проекции линия пересечения состоит из видимой и невидимой частей; видимая часть линии пересечения расположена на обращенных к зрителю видимых гранях. Находящаяся под плоскостью 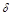 нижняя часть призмы представлена как невидимая. Линия пересечения нарисована лишь на гранях призмы.
нижняя часть призмы представлена как невидимая. Линия пересечения нарисована лишь на гранях призмы.
На рисунке 8 четырехугольная пирамида пересекается плоскостью 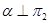 (V). Наклонная площадка
(V). Наклонная площадка 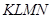 образована срезом верхней части пирамиды фронтально-проецирующей плоскостью
образована срезом верхней части пирамиды фронтально-проецирующей плоскостью 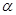 . Фронтальные проекции точек
. Фронтальные проекции точек 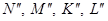 находятся на фронтальном следе плоскости
находятся на фронтальном следе плоскости 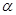 , а фронтальная проекция площадки
, а фронтальная проекция площадки 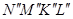 совпадает со следом
совпадает со следом 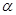 . Профильная проекция
. Профильная проекция 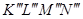 и горизонтальная
и горизонтальная 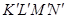 проекции площадки
проекции площадки  построены по проекциям указанных точек на проекциях соответствующих ребер.
построены по проекциям указанных точек на проекциях соответствующих ребер.
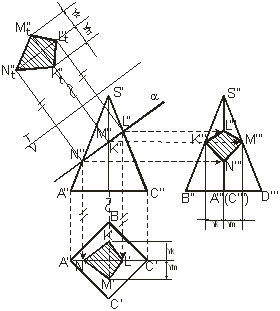
Рис. 8
Для определения натуральной величины сечения вводится плоскость 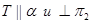 , то есть применяется способ перемены плоскостей проекций. Натуральный вид площадки фигуры сечения – есть четырехугольник
, то есть применяется способ перемены плоскостей проекций. Натуральный вид площадки фигуры сечения – есть четырехугольник 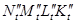 . Все необходимые построения указаны на рисунке 8.
. Все необходимые построения указаны на рисунке 8.
В общем случае в пересечении многогранников получается пространственная замкнутая ломаная линия. При построении линии пересечения многогранников применяют два способа и их комбинации:
1 Строят точки пересечения ребер одного многогранника с гранями другого и ребер второго с гранями первого. Через построенные точки в определенной последовательности проводят ломаную линию пересечения данных многогранников. При этом отрезки прямых проводят лишь через те построенные точки, которые лежат в одной и той же грани.
2 Строят отрезки прямых, по которым грани одной поверхности пересекают грани другой. Эти отрезки являются звеньями ломаной линии пересечения многогранных поверхностей между собой.
Таким образом, исходная задача сводится или к построению линии пересечений двух плоскостей между собой, или к построению точки пересечения прямой с плоскостью. Обе эти задачи уже рассмотрены выше.
 2015-04-17
2015-04-17 4378
4378