Связь между теплоотдачей и трением

Рассмотрим безнапорное течение жидкости с физическими свойствами, не зависящими от температуры, при отсутствии массовых сил. Координатную ось ox направим вдоль поверхности стенки. Безразмерные уравнения движения и энергии для этого случая примут вид:

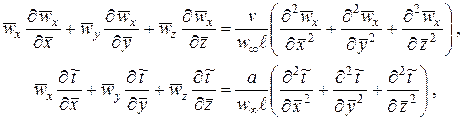(2.16)

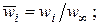
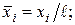
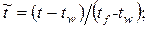
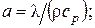
где 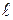- характерный размер; 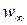- скорость невозмущённого потока; 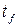- температура жидкости вне пограничного слоя; 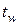- температура стенки.

Граничные условия у этих уравнений одинаковы:

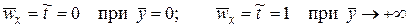. (2.17)

Коэффициенты вязкости 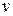и температуропроводности 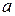в уравнениях (2.16) могут быть равны следующим значениям:

1) при ламирарном режиме течения в пограничном слое

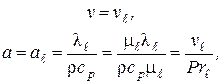
где 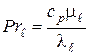- число Прандтля при ламинарном режиме течения;

2) при турбулентном режиме течения в пограничном слое

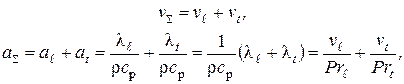
где 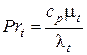- число Прандтля при турбулентном режиме течения.

При ламинарном пограничном слое на пластине и числе 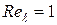коэффициенты вязкости и температуропроводности будут равны:

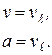
В этом случае уравнения (2.16) становятся тождественными. При одинаковых граничных условиях (2.17) они будут иметь одинаковые безразмерные решения:

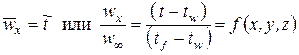. (2.18)

Соотношение (2.18) сохранится и при турбулентном режиме течения, когда 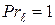и 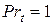, то есть при значениях 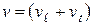и .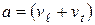

Воспользуемся подобием скоростных и температурных полей для получения количественной связи между интенсивностью теплоотдачи и трением. Для этого определим плотность теплового потока и напряжение трения на поверхности стенки:

.

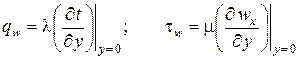Разделив первое уравнение на второе, получим:

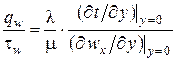. (2.19)

Продифференцировав соотношение (2.18) по координате y, найдём значения производных, входящих в уравнение (2.19):

.

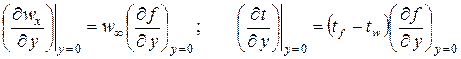Подставив найденные значения производных в формулу (2.19), получим:

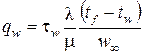. (2.20)

Полученное равенство отражает связь между теплоотдачей и трением и называется аналогией Рейнольдса.

При внешнем обтекании тел напряжение трения определяется через коэффициент трения выражением:

,

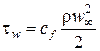а плотность теплового потока 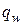- из формулы Ньютона:

.

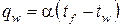Подставив эти значения в формулу (2.20), найдём:

.

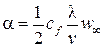Последнюю формулу можно привести к безразмерному виду:

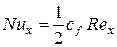, (2.21)

где , .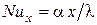

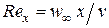Если число 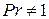, то влияние физических свойств жидкости можно учесть множителем :

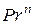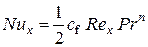(2.22)

При течении жидкости в трубах и каналах температура 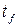и скорость 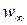в формуле (2.20) заменяются на осреднённые по сечению значения.

Перепад давления связан с напряжением трения выражением:

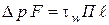, (2.23)

где 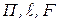- значения соответственно периметра, длины и площади поперечного сечения трубы или канала.

Величину перепада давления в трубе или канале найдём из формулы Дарси-Вейзбаха:

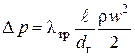, (2.24)

где 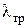- коэффициент сопротивления трения одного калибра трубы; w – среднерасходная скорость; 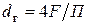- гидравлический диаметр.

Заменив в формуле (2.23) перепад давления его значением (2.24), найдем:

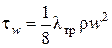. (2.25)

Подставив значение напряжения трения 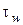из (2.25) и величину плотности теплового потока 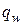, найденную по формуле Ньютона, получим:

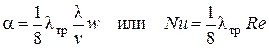, (2.26)

где ; .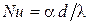

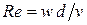При числах 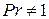формула (2.26) примет вид:

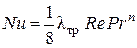. (2.27)

В формулах (2.22) и (2.27) величина n =0,33¸0,43.

Иногда формулы (2.21) и (2.26) записывают в виде:

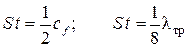. (2.28)

Следует ещё раз отметить, что соотношения (2.20), (2.21) и (2.26) отражают аналогию Рейнольдса.