Доказать, что прямые 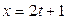 ; ; 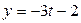 ; ; 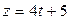 и и 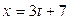 ; ; 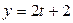 ; ; 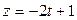 лежат в одной плоскости и составить её уравнения лежат в одной плоскости и составить её уравнения
| 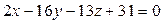
| |
Найти проекцию точки 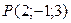 на прямую на прямую 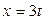 ; ; 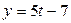 ; ; 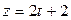
| 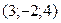
| |
Составить уравнение плоскости, проходящей через точку 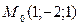 , перпендикулярно к прямой , перпендикулярно к прямой 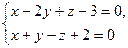
| 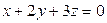
| |
Составить уравнение плоскости, проходящей через начало координат, параллельно прямой 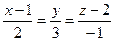 и перпендикулярно к плоскости и перпендикулярно к плоскости 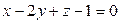
| 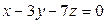
| |
Составить уравнение плоскости, проходящей через прямую 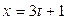 ; ; 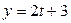 ; ; 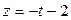 параллельно прямой параллельно прямой 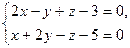
| 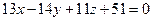
| |
Составить уравнение прямой, проходящей через точку пересечения прямой 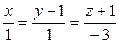 с плоскостью с плоскостью 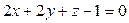 и точку и точку 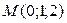
| 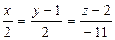
| |
Составить уравнение прямой, проходящей через проекцию точки 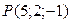 на плоскость на плоскость 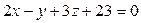 и точку пересечения данной плоскости с осью OY. и точку пересечения данной плоскости с осью OY.
| 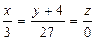
| |
Найти расстояние от точки 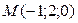 до плоскости, проходящей через до плоскости, проходящей через 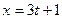 ; ; 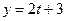 ; ; 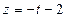 и параллельно прямой и параллельно прямой 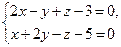
| 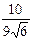
| |
Написать уравнение перпендикуляра, опущенного из точки 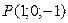 на прямую на прямую 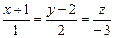
|
Данное пособие способствует повышению интереса к самостоятельной творческой, интеллектуальной деятельности. На это направлена и сама структура пособия. Базовые знания по учебным элементам УЭ.06.02, УЭ.06.03 систематизированы, представлены в виде структурных схем и алгоритмов, что помогает студентам легко анализировать условия задачи, делать постановку задачи и т.д. Дана таблица базовых уравнений, формул и понятий
(приложение А)
Работая с данным пособием, студенты имеют возможность наглядно представлять, воспринимать и осознавать логику взаимосвязей в математике.
Учебно-методическое пособие может быть использовано студентами при выполнение практических работ 18, 19 «Составление уравнений плоскостей и прямых в пространстве», самостоятельной работы студента 17, 18
 2015-06-28
2015-06-28 683
683








